Les mesures
dans les classes du second cycle
R. DECHENE,Inspecteur général de l'Instruction publique.
La mesure est partout. Elle est à la base de toute science : Lord Kelvin, H. Poincaré, Le Dan-tec ont exprimé sous des f o r m e s diverses qu' « il n'est de sciences que du mesurable ». La psycho-logie et la sociopsycho-logie elles-mêmes ne sont deve-nues des- sciences que lorsqu'elles ont été objets de mesures.
La mesure intéresse le théoricien p a r la contri-bution qu'elle apporte à l'accroissement de la connaissance ; elle intéresse le technicien parce que l'accroissement de la précision est à la base de tout progrès technique; elle intéresse enfin le philosophe p a r les problèmes de l'invariabilité des étalons et de l'interaction entre l'objet étudié et l'instrument, tous problèmes qui ne se posaient jusqu'ici qu'à l'échelle quantique et qui pré-sentent désormais un intérêt à un niveau de moindre précision.
A ces problèmes philosophique, technique et scientifique s'ajoute u n problème pédagogique : à une heure où notre enseignement est basé sur l'expérience, il convient de dégager, au niveau de nos classes du second cycle, les principes fonda-mentaux de l'exploitation et de l'interprétation des mesures.
La notion d'incertitude.
L'enfant qui nous arrive en seconde a déjà étudié les sciences naturelles et les mathéma-tiques. Les premières sont surtout p o u r lui des sciences d'observation et les deuxièmes ont u n caractère d'absolu.
Il est f r a p p é par le caractère en apparence approximatif de la physique et c'est dès le début que nous devons lui faire comprendre le sens et la valeur de nos mesures si nous ne voulons pas qu'il considère la physique c o m me la science de « l'à peu près ».
Il f a u t lui faire acquérir rapidement la notion d'incertitude et, si nous ne voulons pas que cette notion reste abstraite, c'est au cours des travaux pratiques qu'il convient de la lui donner.
On commencera p a r des mesures simples, telles que des mesures de longueurs, d'angles, de poids..., où l'on compare la grandeur à u n étalon.
En répétant la mesure de la distance entre deux points bien définis, à l'aide d'une règle gra-duée utilisée c o m m e étalon, on p o u r ra déterminer la « bande d'incertitude » et, p a r suite, la valeur la plus probable de la longueur. Par exemple, si l'on dispose d'une règle graduée en millimètres et si les visées sont correctement faites, les n o m b r e s qui fixent la position de chacun des points ne diffèrent pas entre eux de plus de u n demi-millimètre et la b a n d e d'incertitude pour la distance qui les sépare est de l'ordre du mil-limètre.
De même, avec un r a p p o r t e u r gradué en degrés, la position d'une droite étant définie à un demi-degré près, on p o u r r a mesurer un angle à un degré près.
Mais il ne f a u d r a i t pas généraliser et penser que les incertitudes résultent uniquement des lectures sur l'instrument de m e s u re : il y a aussi l'erreur de « mobilité ». Par exemple, de jeunes professeurs a d m e t t e n t qu'avec les chronomètres dont disposent les élèves de nos établissements qui sont gradués en cinquièmes de seconde, l'incertitude sur la m e s u r e d'un temps est de un cinquième de seconde. Or, l'aiguille de ces chronomètres parcourt la seconde en trois bonds; on ne peut donc espérer repérer u n instant avec une incertitude inférieure à u n tiers de seconde et, p a r conséquent, mesurer u n temps avec une précision meilleure que deux tiers de seconde. Dans un dosage volumétrique, les erreurs résul-tent non seulement des lectures imprécises sur la burette, mais encore de l'erreur de remplis-sage de la pipette et aussi de l'erreur de la goutte qui peut être en excès.
Il convient donc de rechercher toutes les causes d'incertitude et, en particulier, de ne pas éliminer l'équation personnelle qui peut intervenir pour une large part.
Les mesures indirectes.
Lorsque la mesure d'une grandeur résulte des mesures de plusieurs autres auxquelles la pre-mière est liée par une formule, il serait maladroit d'imposer d'autorité, les théorèmes relatifs aux incertitudes.
Le théorème relatif aux incertitudes absolues sur une somme et sur une différence sera faci-lement établi à propos de mesures de périmètres, ou de sommes et de différences d'angles.
Quant aux erreurs relatives sur les produits et les quotients, il conviendra de les faire d'aboi d calculer directement. Par exemple, le domaine d'incertitude sur la surface d'un rectangle sera limité d'une part, par le produit des longueurs des côtés augmentées des incertitudes correspon-dantes (limite supérieure) et d'autre part, par le produit de ces longueurs diminuées des incerti-tudes (limite courte).
On procédera d'une manière analogue à propos de la détermination de jt à partir de la mesure de la circonférence d'un cylindre et de celle de son diamètre.
Les « théorèmes sur les erreurs relatives » vien-dront alors; ils apparaîtront comme une écono-mie, mais quand ils ne sont plus applicables, les élèves auront toujours la ressource d'évaluer directement l'incertitude.
Les grandeurs liées.
On trouve d'ailleurs, dès la classe de seconde, des cas où le théorème des erreurs relatives ne peut être appliqué sans précaution parce que les grandeurs qui figurent dans la formule de déter-mination ne sont pas indépendantes.
C'est ainsi que la mesure de la masse volu-mique d'un solide par la méthode du flacon ou par application du théorème d'Archimède repose sur une relation de la forme
o = e„ P* — Pi
p=~pi
(Ph P=, représentant les poids des masses
mar-quées permettant de réaliser des équilibres clas-siques) dans laquelle la même grandeur pi figure au numérateur et au dénominateur avec le même signe.
Appliquer le théorème sous sa forme habituelle, comme si le numérateur et le dénominateur étaient indépendants, conduirait à un domaine d'incertitude trop étendu car les erreurs sur p^ se compensent partiellement. Cela peut avoir de graves inconvénients s'il s'agit de vérifier une relation comme nous le verrons plus loin; de plus, cela engage l'avenir et risque de donner de mauvaises habitudes aux élèves.
On peut alors faire le calcul direct, c'est-à-dire rechercher les valeurs extrêmes de l'expression
e = e„ (P* ± — (pi ± EQ (p3 ± 8a) — (j?i ± Et)
(ëi = Ea = 8a représentant les incertitudes sur les
poids produisant l'équilibre de la balance) avec toutes les combinaisons de signes possibles, à condition toutefois que ce signe soit le même pour l'incertitude Ei associée à px au numérateur et au dénominateur.
C'est un calcul long dans une classe où les formules d'approximation ne sont pas encore connues (1).
Aussi vaut-il peut-être mieux renoncer à cal-culer l'incertitude dans cette mesure avec les élèves de seconde.
Il existe des cas plus simples où le calcul de l'incertitude est facile. En première, la mesure de la résistance * d'un conducteur à l'aide du pont à corde est basée sur la relation
x = R h , U et U
U
désignant les longueurs découpées par le curseur sur le fil dont la longeur est L = h + U et R la résistance de comparaison.
L'incertitude sur x est donnée par A x A R A Zi jU
x ~ R h/U
Les élèves comprendront bien que si l'erreur sur
h (je dis bien l'erreur) est a, l'erreur sur h est — a;
p a r conséquent, en désignant par 2E le déplacement du curseur ne produisant aucune déviation du gal-vanomètre et en adoptant pour position du curseur la position médiane, les limites du rapport k/U
sont , , , U — E lx + E "7 et U + E U £ limites distantes de 2E + ^ l-f
Ce sont d'ailleurs celles données par le théorème des erreurs relatives.
En classe terminale, on opérera d'une façon ana-logue quand on étudiera la méthode des coïnci-dences qui conduit à la détermination de la période 0 d'un pendule à partir de celle 0O d'un pendule étalonné, en appliquant la formule
© = a N - I
N
Vérification d'une formule.
Contrôler une relation, c'est constater que les mesures des deux membres sont égales.
A cause des erreurs, on ne peut espérer obtenir deux résultats identiques. Leur écart doit être évalué, mais il ne peut servir de conclusion : une
relation ne peut être considérée comme vérifiée que si l'écart réel entre ses deux membres est infé-rieur à l'écart permis.
Prenons un exemple simple. En seconde, on fera vérifier expérimentalement quelques propositions
(1) On p e u t d'ailleurs gagner du t e m p s en calculant l'incertitud e s u r ç — go (ou s u r q0 — p), qui contient u n e f r a c t i o n dont le
n u m e r a t e u r et le d é n o m i n a t e u r r e n f e r m e n t u n e m ê m e g r a n d e u r , mais affectée de signes différents.
mathématiques telles que le théorème relatif à la somme des angles d'un triangle. Si les rapporteurs dont on dispose permettent d'évaluer les angles à un degré près, le domaine d'incertitude sera de 6° : on pourra considérer que le théorème est véri-fié si la somme S trouvée ne diffère de 180" de plus de 3", ou, ce qui revient au même, si le domaine S —3°, S + 3° comprend à son intérieur la valeur 180" (fig. 1). C'est ainsi que des sommes égales à 177° ou à 183° sont cohérentes et égale-ment acceptables.
18 O'
S s * 3 F I G . 1.
Si, ensuite, on donne aux élèves des rapporteurs permettant d'évaluer les angles à 30' près, les limites permises sont 178° 30' et 181° 30'; si l'un d'eux trouve encore 183°, il n'a pas vérifié le théo-rème bien que l'écart relatif soit le même que tout à l'heure.
Il conviendra de rechercher les causes de cette mauvaise mesure : rapporteur mal utilisé, triangle mal défini, trop petit...; on montrera qu'avec des précautions supplémentaires (tracés plus fins) et des instruments plus sensibles (rapporteur gradué en quart de degré, visée par loupe...), on peut réduire le domaine d'incertitude. On donnera ainsi à l'élève le goût du travail bien fait et, en même temps, on lui montrera les limites de nos possi-bilités.
Plus généralement, on ne pourra conclure que la relation A = B est vérifiée que si les domaines
d'incertitude A±a et B ±b ont une partie
com-mune. Tant que ce travail ne sera pas fait, la
manipulation ne sera pas terminée.
Par exemple, demandons à nos élèves de pre-mière de vérifier la loi de l'association des résis-tances en série. Supposons qu'au pont à corde, les incertitudes dépendant de la position du curseur sur le fil, on ait trouvé comme valeurs des résis-tances de deux conducteurs :
r = (10,2 ±0,2) Q
r = (20,1 ± 0,2) Q
et pour le conducteur formé par leur association R = (30,5 ± 0,3) Q.
La somme r. + n sera comprise dans un domaine dont les limites sont 29,9 Q et 30,7 Q et que nous appellerons « domaine calculé ». La résistance du conducteur unique formé par l'association des deux autres sera comprise dans le domaine 30,2 Q — 30,8 Q que nous appellerons « domaine mesuré ». Ces deux domaines ayant une partie commune (fig. 2), la relation R = r, + n pourra être consi-dérée comme vérifiée.
A de tels exemples, montrant l'intérêt de la détermination du domaine d'incertitude et la
néces-2 9 , 9 3 0 , 7 domaine caJcu/é
dcn C7//5 e mesuré
3 0 , 2 3 0 , 8
F I G . 2 .
sité de le réduire, on peut associer celui, historique, de la preuve de l'existence des gaz rares dans l'air. Cette preuve ne f u t établie, à la fin du XIXE siècle,
qu'à partir du moment où l'on remarqua que l'écart entre la masse volumique de l'azote atmos-phérique et celle de l'azote pur préparé au labo-ratoire (environ 1/200) était supérieur au double de l'incertitude (environ 1/1 000) sur la mesure de ces masses.
L'établissement ou le contrôle d'une loi.
L'établissement et le contrôle d'une loi phy-sique — tout au moins de celles qui figurent à nos programmes — se font suivant un processus relativement simple qui ne varie guère d'une loi à une autre et dont il convient de dégager les diverses phases pour donner une méthode à de futurs chercheurs.
Prenons, par exemple, la loi de Mariotte, une des premières grandes lois étudiées en seconde. A l'aide d'un dispositif expérimental classique que l'on peut leur faire découvrir, les élèves feront les mesures de la pression p et du volume v cor-respondant et détermineront les incertitudes sur ces grandeurs. Puis, ils rassembleront les résultats en un tableau.
Il est essentiel qu'ils les reportent sur un gra-phique, d'une part pour avoir une représentation
de la loi, d'autre part, pour éliminer les mesures aberrantes.
La courbe étant l'outil fondamental du physi-cien, on pourrait se contenter de ce résultat et, en fait, on est souvent obligé de s'arrêter à ce stade : il ne saurait être question de représenter par une équation simple la courbe d'aimantation d'un fer ou une caractéristique d'une triode.
Pourtant, notre esprit ne sera satisfait que si l'on peut traduire par une relation mathématique la courbe obtenue et nous devons nous efforcer d'y parvenir.
Remarquons d'ailleurs l'arbitraire de n o t r e choix:
nos mesures sont entachées d'erreurs et à l'une d'elles, correspond non pas un point mais un petit rectangle qui représentera le domaine d'incer-titude.
Les courbes qui traversent tous ces rectangles sont également valables; celle que nous adopterons devra satisfaire à la fois aux exigences des mesures
et à notre souci de simplicité. _ ,
Ici, le fait que le volume est sensiblement divise par deux quand la pression est doublée suggère l'idée que la loi pourrait bien être représentee par l'équation p = k/v.
C'est là une hypothèse qu'il s'agit de vérifier : /autrement dit, il convient d'examiner comment les points expérimentaux se placent par rapport à une hyperbole.
Or, et c'est là une idée fondamentale, le physi-cien ne sait construire que des droites. Il s'agira donc de trouver un changement de variables qui transforme la loi hyperbolique en une loi linéaire. Le problème est facile à résoudre ici : il suffit de poser y = pv. Si la courbe est une hyperbole dans le diagramme de Clapeyron (v, p), elle sera une droite d'ordonnée constante dans le diagramme d'Amagat (p, pv).
Il conviendra d'évaluer l'incertitude sur le pro-duit pv à partir de celles sur p et sur v; chaque petit rectangle est pratiquement assimilable à un segment de droite.
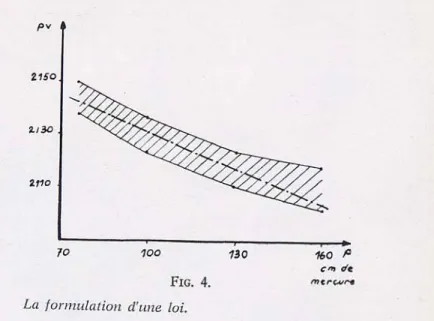
Le lieu des points limites de ces domaines quand la pression p varie constitue la bande d'incertitude. Si, dans cette bande, on peut loger une droite horizontale, nous conclurons qu'on peut repré-senter le produit pv par une constante quand la pression varie, c'est-à-dire que notre hypothèse initiale, la loi de Mariotte, est vérifiée.
Il en est ainsi lorsque le gaz étudié est l'air dans un domaine de pressions compris entre 0 et 2 atmosphères (fig. 3); mais si, dans le même domaine, on opère avec du butane, on ne pourra plus loger une droite horizontale à l'intérieur de la bande d'incertitude. Il faut rechercher une autre loi de compressibilité; on envisagera la plus sim-ple : la mise en place d'une droite oblique étant possible, la loi de compressibilité du butane sera
F I G . 3.
Si, maintenant, on opère dans un domaine de pressions plus étendu, aucune droite n'est plus logeable dans la bande d'incertitude et on devra rechercher une autre équation d'état telle que celle de Van der Waal qui, dans un domaine res-treint de pressions faibles, n'exclut pas la loi linéaire de Mariotte (y = pv) = constante.
Ce mécanisme en deux temps : le tracé de la courbe et la détermination de son équation par transformation linéaire est d'ailleurs celui que l'on utilise sans le dire —- quand, en première, on étu-die la loi de Joule ou, en classe terminale, la loi de la chute des corps et les lois du pendule.
c"t dt
FIG. 4 . MTRCA/R*
La formulation d'une loi.
La loi doit être présentée sous sa forme la plus naturelle, la plus concrète et la plus suggestive L expression linéaire que l'on a obtenue par chan-gement de variables n'est pas toujours la plus accessible; par exemple, il vaut mieux énoncer la loi de Mariotte sous la forme :
A une température donnée, le volume d'une masse donnée de gaz est inversement proportionnel à sa pression.
Plutôt que sous la forme :
Le produit des nombres qui mesurent la pres-sion et le volume d'une masse donnée de gaz a température fixe est constant.
A ce propos, il me paraît opportun d'énoncer la loi de conjugaison des lentilles minces sous la forme :
La convergence du faisceau émergent est égale à la convergence du faisceau incident correspon-dant augmentée de la convergence de la lentille,
qui traduirait le véritable rôle d'une lentille, à savoir, celui de modifier d'une quantité constante caractéristique de la lentille, la convergence des faisceaux qu'elle reçoit.
Sans doute, certains professeurs regretteront-ils que cet énoncé ne fasse pas sa place à la fonction homographique; mais que penseraient-ils si j'énon-çais la loi de Mariotte sous la forme : Log p + Log v = constante, sous prétexte cle montrer une application de la fonction logarithmique ?
L'abus des moyennes.
On ne doit adopter comme valeur probable d'une grandeur la valeur moyenne d'une série de mesures que dans des conditions très restrictives.
On peut attribuer une signification à la moyenne quand elle correspond à un grand nombre de me-sures d'un même phénomène réalisées dans les mêmes conditions, ou des conditions très voisines, par un même individu.
C'est ainsi qu'en répétant plusieurs fois, avec le même instrument, la mesure d'une longueur,
d'un temps, d'un angle..., on pourra définir le domaine d'incertitude à partir du calcul de l'écart
moyen. Ce procédé est d'ailleurs le seul qui soit
utilisable pour déterminer la précision de mesures purement subjectives telles que les mesures photo-métriques.
Dans les autres cas, il est imprudent de faire calculer « la moyenne » et téméraire de l'utiliser. — D'abord, la moyenne de mesures, faites avec le même instrument, par des individus différents est sujette à caution : il ne viendrait à l'idée de personne de mélanger les résultats obtenus dans une expérience d'acoustique par un sourd et une « fine oreille ».
—• La moyenne de mesures correspondant à des « poids » différents est aussi sans valeur. De jeunes professeurs, étudiant la chute ralentie d'un mobile le long d'un plan incliné, calculent l'accélération en mélangeant les résultats, peu précis, obtenus pour de faibles hauteurs de chute (et par consé-quent pendant de faibles durées de chute) avec celles, bien meilleures, relatives aux grandes
dis-tances, donc aux grandes durées.
Le tracé de la bande d'erreur relative à la quan-tité y = e/Z2, tel que celui de la figure 5 qui résulte d'une expérience de classe, montre que la valeur la plus probable de cette grandeur est l'ordonnée de la médiatrice de cette bande dans sa partie la plus étroite.
y-•/*«
\alcor* lo
pjuj /oroboble
F I G . 5 .
— A fortiori, il n'est pas raisonnable de faire la moyenne de résultats trouvés par des élèves différents travaillant avec des instruments diffé-rents. Tout au plus, convient-il de contrôler que les résultats obtenus sont cohérents. Deux exem-ples vont illustrer cette maladresse.
J'assistais un jour à la détermination, en tra-vaux pratiques, de la masse volumique o de solu-tions sodées en fonction de leur titre t connu par la méthode classique des dénivellations. Un tube en U (fig. 6) dont la branche de gauche plon-geait dans l'eau et la branche de droite dans la solution étudiée, portait un ajutage par lequel on aspirait jusqu'à ce que l'eau atteigne un trait de repère A ; la mesure de la hauteur d'ascension
J L
eau
F I G . 6.
h'epui'de ef-uah'*'
du liquide dans l'autre tube conduisait facilement à la valeur de sa masse volumique.
Pour cette mesure, certains groupes disposaient de réglets d'acier; d'autres, de règles à dessin; d'autres enfin, de planchettes sur lesquelles on avait collé du papier millimétrique. Or, je m'aper-çus que, par suite de l'allongement de ce papier au cours de son collage, ces derniers instruments conduisaient à une erreur systématique d'environ 3 %.
Un groupe d'élèves, qui manipulait fort soigneu-sement, trouva avec sa règle défectueuse, une courbe q = f (T) très différente de celles des autres groupes. Le professeur fit afficher les résultats au tableau et tracer une « courbe moyenne », laquelle — et c'est là le plus grave — devait être utilisée en sens inverse, c'est-à-dire à la détermination du titre d'une solution inconnue à partir de son poids volumique. En utilisant sa propre courbe, le groupe à la règle fausse aurait pu obtenir un résultat exact puisqu'il y avait cohérence entre l'opération directe et l'opération inverse; utilisant la courbe type, ses résultats furent les plus mauvais. Son travail, sérieux, fut le plus mal payé.
Voici un deuxième exemple. Au cours d'épreuves pratiques du Capes, un candidat eut l'intention de faire déterminer la valeur F du Faraday (F = 96 500 coulombs) à partir de la mesure du volume de gaz dégagé dans une électrolyse par un courant dont l'intensité était lue sur un ampèremètre. Sans se soucier de l'incertitude sur les mesures, il fit faire la moyenne des résultats obtenus par les dix groupes de travail, résultats que je reproduis i c i : 96 000; 95 800; 95 300; 97 000; 95 600; 95 400; 97 200 ; 95 500 ; 95 800 ; 96 000, ce qui conduisit à la moyenne 95 860.
Suivant une tradition déplorable, il fit calculer l'écart moyen : 384, ce qui conduisit à la double inégalité 95 480 < F < 96 240.
La séance de travaux pratiques précédait la leçon; je me demande quelle confiance les élèves auront eue en leurs travaux quand le lendemain ils se seront aperçus que la valeur adoptée aujour-d'hui ne vérifie pas cette double inégalité.
Il eût fallu déterminer pour chaque groupe la bande d'incertitude, en tenant compte du fait que 42
courba c cccyr 6e f^ioy *nn «
F I G . 7 .
•> c
les ampèremètres étaient de classe 2 et que les éprouvettes étaient graduées en dixièmes de centi-mètres cubes, ce qui correspondait à une incerti-tude d'environ 2 %.
Le graphique 8, que l'on peut faire tracer au tableau à partir des résultats des divers groupes, montre que toutes ces bandes ont une partie com-mune : les mesures sont donc cohérentes. Les frontières de cette partie commune étant 95 200 et 97 300, en adoptant la valeur médiane 96 250, on peut espérer avoir une détermination exacte à 1 %. Le travail en équipe aura eu pour résultat de réduire l'incertitude d'environ la moitié de sa valeur.
— Enfin, une moyenne masque souvent une variation systématique. Un professeur, faisant déterminer la constante de torsion d'un fil par la méthode statique, adoptait comme valeur la plus probable la moyenne des quotients C/0. C dési-gnant le couple obtenu avec deux masses marquées et produisant la torsion 0.
A ma demande, on traça la courbe C = / (©) et
98ooo 9/000 9 iooo
95ooo
F I G . 8.
l'on s'aperçut que si elle pouvait être assimilée à une droite, elle ne passait pas par l'origine, ce que Ion expliqua en remarquant que l'on n'avait Pas tenu compte du poids des plateaux suppor-tant les masses marquées. Les rapports représen-taient non pas la constante de torsion du fil, mais
es pentes variables des cordes joignant l'origine coordonnées aux divers points de la droite.
Cela constitue une justification supplémentaire de la nécessité de construire, avant tout calcul, les courbes représentant les résultats des mesures.
La rigueur dans la conception de la mesure.
Si nous voulons que nos élèves aient foi en l'ex-périence, apportons autant de rigueur dans le rai-sonnement expérimental que dans le rairai-sonnement théorique fait au tableau noir.
Sous prétexte de gagner du temps, un professeur qui voulait vérifier, dans une expérience sur l'élec-trolyse, que le volume gazeux dégagé à la cathode d'un électrolyseur est proportionnel au temps de passage du courant, tenait à peu près ce langage : « Lançons le courant et coupons l'interrupteur après une minute; mesurons le volume v de gaz; lançons à nouveau le courant pendant une nouvelle minute au cours de laquelle le volume dégagé est v'; nous admettrons que pendant deux minutes le volume dégagé est v + v'... »
Il ne s'apercevait pas qu'il admettait a priori une loi linéaire. Supposons en effet qu'un de ses élèves, au cours d'une étude de la chute des corps, fasse le raisonnement suivant : « Lâchons une bille en un point d'un plan incliné et arrêtons-la après une seconde au cours de laquelle elle aura parcouru l; lâchons-la à nouveau pendant une nouvelle seconde au cours de laquelle elle par-court l\ peu différent de l; nous admettrons qu'après deux secondes de chute, la bille aurait parcouru l + V soit sensiblement 2 l... Nous pour-rons en conclure que la chute obéit à la loi e : t — constante. »
/ / C^. ; Conshonï* de horsic
~T~
— —
F I G . 9.
Que faut-il conclure ?
Si la mesure est à la base de toute science, elle ne conduit pas nécessairement à la connaissance; elle n'est qu'un auxiliaire qui ne peut à lui seul contenter l'esprit.
Si l'on veut qu'elle ait une valeur culturelle, il f a u t qu'elle soit pensée, aussi bien dans sa réali-sation que dans son interprétation.
Cela doit être un principe de notre éducation scientifique élémentaire.