Regroupement optimal d’objets à l’intérieur d’un
nombre imposé de classes de taille égale
Mémoire
David Emond
Maîtrise en statistique
Maître ès sciences (M. Sc.)
Résumé
Dans ce mémoire, on considère la situation où l’on désire grouper des objets dans un nombre prédéterminé de classes de même cardinal. Le choix de la composition des classes est basé sur des critères de minimisation de la variance intragroupe ou de maximisation de la similarité intragroupe. Trois méthodes sont développées pour obtenir le regroupement optimal selon l'un de ces critères. Les deux premières approches consistent à diviser le problème global de classification en plusieurs sous-problèmes, respectivement selon les valeurs prises des variables d’intérêt et selon un aspect probabiliste. La troisième méthode utilise des propriétés de la loi stationnaire des chaînes de Markov. Les trois techniques sont utilisées pour tenter de trouver le regroupement optimal pour classer géographiquement les équipes de la Ligue nationale de hockey en six divisions de cinq équipes. Des études de simulation permettent de mesurer l'efficacité des méthodes.
Abstract
This master's thesis is structured around the case in which we want to classify objects into a specific number of clusters of the same size. The choice of clusters to form is determined by minimizing the within-cluster variance or maximizing the within-within-cluster similarity. Three methods were developed to obtain the optimal clustering according to these two criterions. The first two approaches consist in splitting up the clustering problem in several sub-problems, one in a quantitative way and the other in a probabilistic way. The third method uses properties of the Markov chain limiting probabilities. The three methods are used to try to find the optimal geographic clustering to class the thirty National hockey league teams into six divisions of five teams. The efficiency of those approaches is assessed with simulations.
Table des matières
Résumé ... iii
Abstract ... v
Table des matières ... vii
Liste des tableaux ... ix
Liste des figures ... xiii
Remerciements ... xvii
Introduction ... 1
1.
Définition des critères d'optimisation ... 7
2.
Présentation du jeu de données ... 9
3.
Examen du cas du partitionnement à une seule variable d'intérêt ... 11
4.
Présentation de l'approche algorithmique ... 13
5.
Présentation de l’approche probabiliste ... 25
6.
Introduction aux chaînes de Markov ... 31
7.
Présentation de l'approche markovienne ... 37
8.
Étude de simulations ... 53
Conclusion ... 61
Bibliographie ... 65
A.
Démonstration de la formule 1.1 ... 67
Liste des tableaux
Tableau I.1 - Ordre du nombre de regroupements possibles de n objets en c groupes de même
cardinal k ... 2
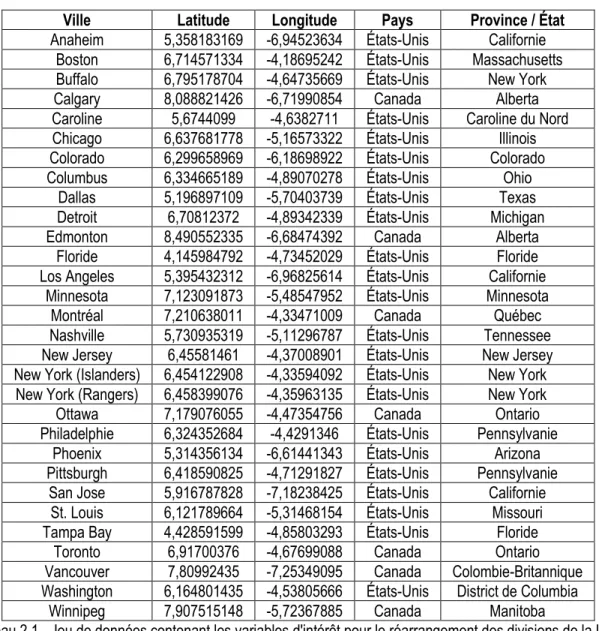
Tableau 2.1 - Jeu de données contenant les variables d'intérêt pour le réarrangement des
divisions de la Ligue nationale de hockey ... 10
Tableau 3.1 - Réarrangement optimal des divisions de la Ligue nationale de hockey avec
« Latitude » comme seule variable d’intérêt ... 11
Tableau 3.2 - Un des réarrangements optimaux des divisions de la Ligue nationale de hockey
avec « Pays » comme la seule variable d’intérêt ... 12
Tableau 4.1 - Combinaisons de sous-populations permettant de classer trente objets en six
groupes de cinq objets ... 15
Tableau 4.2 - Séparation de la population en sous-populations selon la variable « Latitude »
pour la quatrième combinaison du tableau 4.1 ... 17
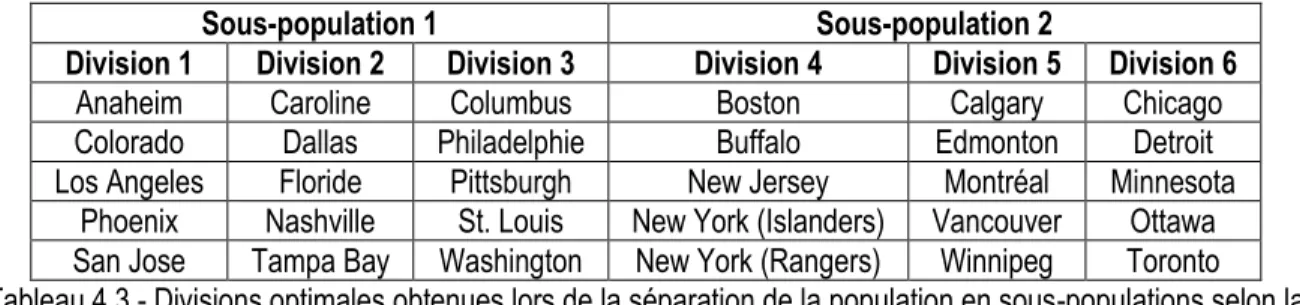
Tableau 4.3 - Divisions optimales obtenues lors de la séparation de la population en
sous-populations selon la variable « Latitude » pour la quatrième combinaison du tableau 4.1 ... 18
Tableau 4.4 - Séparation de la population en sous-populations selon la variable « Longitude »
pour la quatrième combinaison du tableau 4.1 ... 18
Tableau 4.5 - Divisions optimales obtenues lors de la séparation de la population en
sous-populations selon la variable « Longitude » pour la quatrième combinaison du tableau 4.1 ... 18
Tableau 4.6 - Indices de similitude obtenus lors de la séparation de la population en
sous-population selon les deux variables quantitatives en considérant toutes les combinaisons du
tableau 4.1 ... 19
Tableau 4.7 - Variance intraclasse obtenue pour les deux variables quantitatives en considérant
toutes les combinaisons du tableau 4.1 ... 20
Tableau 4.8 - Divisions optimales d’un point de vue de la minimisation de la variance intraclasse
obtenues lors de la séparation de la population en sous-populations ... 20
Tableau 4.9 - Jeu de données contenant deux nouvelles variables permettant d'expliciter le
traitement des égalités et des variables catégoriques dans la méthode algorithmique ... 21
Tableau 4.10 - Séparation de la population en sous-populations selon la variable « Rang »
considérant la variable « Latitude » comme variable de « bris d'égalité » pour la quatrième
combinaison du tableau 4.1 ... 22
x
Tableau 5.1 - Partitionnement optimal des objets sélectionnés lors d’un premier échantillon de
quinze individus ... 27
Tableau 5.2 - Divisions obtenues lors d’un premier partitionnement basé sur l’approche
probabiliste ... 28
Tableau 5.3 - Divisions optimales d’un point de vue de la maximisation de l'indice de similitude
intraclasse obtenues par l'approche probabiliste ... 28
Tableau 5.4 - Divisions optimales d’un point de vue de la minimisation de la variance intraclasse
obtenues par l'approche probabiliste ... 29
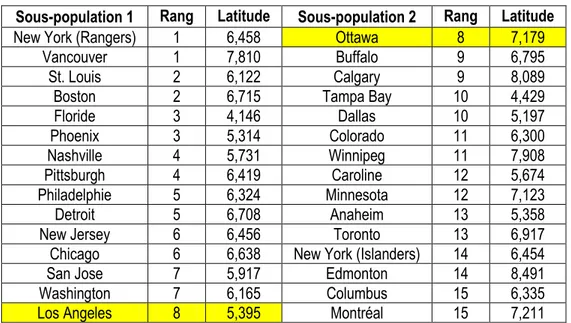
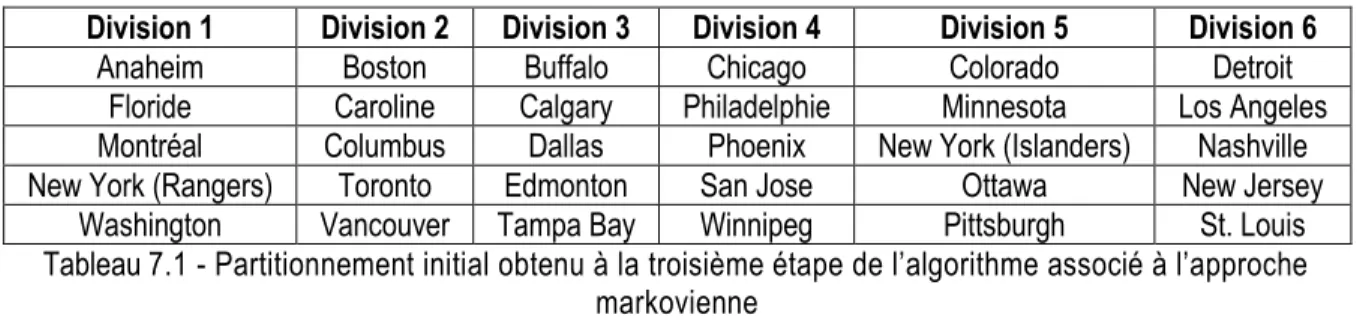
Tableau 7.1 - Partitionnement initial obtenu à la troisième étape de l’algorithme associé à
l’approche markovienne ... 42
Tableau 7.2 - Poids quantifiant la différence entre chaque équipe et les équipes de son
groupe initial ... 43
Tableau 7.3 - Poids considérant trois mesures de similarité pour chaque observation ... 43
Tableau 7.4 - Partitionnement localement optimal obtenu après un premier partitionnement
initial de l’approche markovienne ... 44
Tableau 7.5 - Divisions optimales d’un point de vue de la maximisation de l'indice de similitude
intraclasse obtenues par l'approche markovienne ... 45
Tableau 7.6 - Divisions optimales d’un point de vue de la minimisation de la variance
intraclasse obtenues par l'approche markovienne ... 45
Tableau 7.7 - Ensemble des regroupements de quatre objets en deux classes de deux individus ... 46
Tableau 8.1 - Catégories des caractéristiques des jeux de données simulés ... 53
Tableau 8.2 - Caractéristiques des jeux de données simulés... 54
Tableau 8.3 - Valeur des indices d’optimalisation associés au regroupement « optimal »
proposé par les trois approches de partitionnement pour chaque jeu de données simulé ... 55
Tableau C.1 - Divisions optimales d’un point de vue de la minimisation de la variance
intraclasse des coordonnées géographiques des villes de la Ligue nationale de hockey ... 63
Tableau A.1 - Exemple de deux regroupements équivalents ... 67
Tableau B.1 - Matrice du nombre de fois où les équipes ont été sélectionnées dans un même
échantillon dans le cas de la maximisation de l’indice de similarité intraclasse ... 69
Tableau B.2 - Matrice du nombre de fois où les équipes sélectionnées dans un même
échantillon ont été classées dans un même groupe dans le cas de la maximisation de l’indice de
similarité intraclasse ... 70
Tableau B.3 - Matrice de la probabilité pour des équipes sélectionnées dans un même
échantillon soient classées dans un même groupe dans le cas de la maximisation de l’indice de
similarité intraclasse ... 71
Tableau B.4 - Matrice du nombre de fois où les équipes ont été sélectionnées dans un même
échantillon dans le cas de la minimisation de la variance intraclasse ... 72
Tableau B.5 - Matrice du nombre de fois où les équipes sélectionnées dans un même
échantillon ont été classées dans un même groupe dans le cas de la minimisation de la
variance intraclasse ... 73
Tableau B.6 - Matrice de la probabilité pour des équipes sélectionnées dans un même
échantillon soient classées dans un même groupe dans le cas de la minimisation de la variance
intraclasse... 74
Liste des figures
Figure 4.1 - Permutations possibles de la taille des sous-populations dans le cas de la
huitième combinaison du tableau 4.1 ... 16
À Andréanne, la petite fille de ma vie! Pour
te signifier tout l’amour que j’ai pour toi et
pour te remercier de rendre ma vie si
parfaite!
Remerciements
Ce mémoire signifie la fin de mes études postsecondaires au département de mathématiques et de statistique de l'Université Laval. C'est donc avec une certaine nostalgie que je mets au jour le fruit de mes recherches. Évidemment, c'est aussi avec une grande fierté et avec le sentiment du devoir accompli que je vous présente ce document.
Je désire d'abord remercier Madame Nadia Ghazzali, ma directrice de maîtrise, de m'avoir encadré tout au long de ma recherche malgré son horaire très chargé. Je remercie également les autres professeurs et les chargés de cours en statistique du département pour toutes les connaissances mathématiques et statistiques qu'ils m'ont permis d'acquérir tout au long de mes études universitaires. Plus particulièrement, je remercie Mesdames Sophie Baillargeon et Anne-Catherine Favre ainsi que Messieurs Claude Bélisle, Alexandre Bureau, Michel Carbon, Thierry Duchesne, Christian Genest, Rachid Kandry Rody, M'Hamed Lajmi Lakhal Chaieb, Jean-Claude Massé et Louis-Paul Rivest. Je désire de plus exprimer ma reconnaissance à Monsieur Gaétan Daigle et à Madame Hélène Crépeau pour les compétences pratiques en statistique qu'ils m'ont transmises lors de l'exécution de mon projet de fin d'études au baccalauréat et lors des réunions hebdomadaires du Service de consultation statistique. Monsieur Denis Talbot mérite lui aussi un énorme remerciement de ma part. En effet, je ne peux que le considérer comme étant officieusement mon codirecteur de maîtrise. Monsieur Talbot m'a beaucoup aidé à optimiser mes programmes informatiques développés en lien avec ma recherche. Il m'a également conseillé tout au long de mes études de maîtrise. Grâce à tous ces gens, je serai, je l'espère, un excellent statisticien professionnel!
Je ne veux pas passer sous silence l'apport de mes parents et de mes deux frères tout au long de mes études primaires, secondaires, collégiales et universitaires. Mes parents, Magella et Thérèse, m'ont d'abord inculqué dès le plus jeune âge le sérieux nécessaire à ma réussite scolaire. Ils m'ont aussi toujours accompagné et encouragé durant mes études. C'est pourquoi je les remercie grandement, car, sans eux, je n'aurais jamais aussi bien réussi tout au long de mon parcours scolaire et je ne serais pas devenu la personne que je suis actuellement. Pour ce qui est de mes deux frères, Jérôme et Samuel, je les remercie d'être des personnes aussi performantes et aussi fonceuses. Ainsi, connaissant la très forte, mais surtout la très saine compétition qu'il existe entre eux et moi, je n'ai eu, moi aussi, d'autres choix que de me surpasser dans l'ensemble des projets que j'ai entrepris jusqu'ici. Vous êtes des exemples pour moi, mais surtout des idéals à atteindre!
xviii
Je tiens enfin à souligner que l'exécution de mes travaux s'est toujours faite dans la joie et dans le plaisir. Comme vous pourrez le constater à la lecture de mon document, mon sujet de mémoire peut s'appliquer à un possible remaniement des divisions de la Ligue nationale de hockey. Étant un grand amateur de ce sport, il va sans dire que je n'ai jamais manqué de motivation lors de l'élaboration de mes méthodes de classification. J'étais aussi toujours très curieux de voir les regroupements d'équipes que mes méthodes me proposaient. J'espère que cet esprit de curiosité vous habitera tout au long de la lecture de mon mémoire. Vous pourrez ainsi éprouver autant de plaisir à lire le document que j'en ai eu à faire mes recherches.
Introduction
Lors de l'été 2011, le commissaire de la Ligue nationale de hockey, Monsieur Gary Bettman, annonçait que l'équipe des Thrashers d'Atlanta avait été vendue à True North Sports and Entertainment. Le but principal de cette compagnie winnipegoise était de déménager la formation sportive dans la capitale du Manitoba. Ce transfert de l'équipe d'une ville du sud-est des États-Unis dans une ville canadienne implique un réarrangement des divisions de la Ligue nationale de hockey (DION, 2011). Pour ce faire, il faudra développer des approches conçues pour trouver un remaniement optimal des divisions.
Afin de bien comprendre la problématique de la restructuration des divisions de la Ligue nationale de hockey, il faut d'abord savoir que cette ligue compte trente équipes dont le domicile est situé en Amérique du Nord. Les équipes sont divisées en deux conférences de quinze équipes, soit la conférence de l'Est et la conférence de l'Ouest. Trois divisions de cinq équipes sont incluses dans chacune des deux conférences. La conférence de l'Est contient la division Atlantique, la division Nord-Est et la division Sud-Est. La division Centrale, la division Nord-Ouest et la division Pacifique sont, quant à elles, incluses dans la conférence de l'Ouest (LIGUE NATIONALE DE HOCKEY, 2012). Chaque année, les équipes d'une même division jouent six parties les unes contre les autres. Quatre rencontres sont prévues au calendrier pour les équipes de la même conférence n'appartenant pas à la même division. Les équipes de conférences différentes s'affrontent, quant à elles, à une ou à deux reprises par saison (LEBRUN, 2007). Ainsi, pour minimiser les déplacements lors de la saison régulière de hockey, les équipes d'une même division ont tout avantage à être situées à proximité les unes des autres. Il devient donc intéressant d'essayer de trouver les six divisions de cinq équipes qui minimisent la variance intradivision des coordonnées géographiques des villes ayant sur leur territoire une équipe de la Ligue nationale de hockey.
A priori, il semble facile d'obtenir ce regroupement optimal des trente formations de la Ligue nationale de hockey en six groupes de cinq équipes. Effectivement, il suffirait de considérer l'ensemble des possibilités de groupements, de calculer leur variance intradivision et de retenir la combinaison avec la variance minimale. Cette solution, en théorie, très simple, est cependant impossible à considérer en pratique. En effet, malgré la rapidité de calcul et la mémoire des ordinateurs modernes, il faudrait plus d'un million d'années à un ordinateur muni d’un processeur de 4,1 gigahertz pour obtenir l'ensemble des six divisions de cinq équipes qu'il est possible de former. En fait, le nombre de possibilités est de l'ordre de 1017. Le tableau suivant montre
l'ordre du nombre de regroupements possibles de n objets en c groupes de même cardinal k pour certains nombres n sélectionnés.
2 n 1 2 3 4 5 6 c 8 9 10 15 20 30 4 100 100 100 6 100 101 101 100 8 100 101 102 100 9 100 102 100 10 100 102 102 100 20 100 104 108 109 108 100 30 100 107 1011 1016 1017 1018 1015 100
Tableau I.1 - Ordre du nombre de regroupements possibles de n objets en c groupes de même cardinal k Le tableau I.1 permet de voir que le nombre de groupements peut être très élevé malgré une quantité relativement faible d'objets à classer. Le nombre de regroupements possible de n objets en c groupes de taille
k peut être calculé à l'aide la formule suivante démontrée à l'annexe A.
( ) ( ) Comme il a été mentionné précédemment, il est impossible de vérifier rapidement et avec certitude l'arrangement des divisions de la Ligue nationale de hockey qui minimise la variance intradivision. Il devient donc nécessaire d'imaginer et de développer de nouvelles techniques de classification pour remédier à cette situation problématique. Il est à noter que quelques méthodes conçues spécifiquement pour regrouper des objets en un certain nombre de classes de même taille ont déjà été développées. Notons par exemple les algorithmes présentés par BANERJEE et GHOSH (2002), par KLAWONN et HÖPPNE (2006), par ZHU, WANG et LI (2010) ainsi que par ELLIOT (2011). Ces algorithmes ne seront pas présentés dans le présent document. Les références sont fournies à titre indicatif seulement. De plus, les nouvelles méthodes de classification présentées dans ce mémoire ont été développées de façon tout à fait indépendante des quatre algorithmes élaborés par les personnes nommées précédemment.
Afin de bien comprendre les techniques de classification élaborées dans le présent document, une brève introduction à la classification peut être utile. Le principal objectif de la classification est de réunir à l'intérieur de classes les objets similaires d'un ensemble et de placer dans des classes distinctes les objets différents du même ensemble . Pour quantifier la ressemblance ou la différence entre deux éléments de cet ensemble, on peut calculer une distance ou une similarité. Ces deux indices des ressemblances sont des applications de à valeurs numériques qui associent, pour tout élément ( ) appartenant à , un nombre mesurant le lien entre et (GHAZZALI, 2010).
Définition I.1 : Une distance sur un ensemble est une application de dans qui vérifie les quatre propriétés suivantes.
a) ( ) ( ) ; (Propriété de non-négativité de ) b) ( ) ( ) ( );
(Propriété de symétrie de )
c) ( ) ( ) ;
(Propriété de minimalisation de en cas d'identité de deux objets) d) ( ) ( ) ( ) ( ).
(Propriété de respect de l'inégalité triangulaire de ) (GHAZZALI, 2010)
Définition I.2 : Un indice de similarité sur un ensemble est une application de dans qui vérifie les trois propriétés suivantes.
a) ( ) ( ) ; (Propriété de non-négativité de ) b) ( ) ( ) ( );
(Propriété de symétrie de )
c) ( ) ( ) ( ) ( ).
(Propriété de maximalisation de en cas de similarité d'un objet avec lui-même) (GHAZZALI, 2010) Il est possible de calculer un indice de similarité à partir d'une mesure de distance. La réciproque n'est cependant pas vraie en raison de l'inégalité triangulaire (GHAZZALI, 2010).
Il existe trois principaux types de classification. Plus particulièrement, il y a le partitionnement ou la classification non hiérarchique, la classification hiérarchique et la classification bayésienne. Le partitionnement a pour but de classer n objets en c classes disjointes selon un critère d'adéquation. La composition des classes est déterminée par le partitionnement optimisant ce critère. Les critères d'adéquation peuvent se séparer en deux principales catégories, soit les critères d'hétérogénéité ou de manque de cohésion d'une classe et les critères d'isolation ou de séparation d'une classe par rapport aux autres objets. La minimisation de la somme des variances intrapartition et la minimisation de la distance entre les objets d'une même partition sont deux exemples de critères d'hétérogénéité. Un cas particulier d'un critère d'isolation peut être la maximisation des distances entre les objets d'une classe et les objets à l'extérieur de cette classe (GORDON, 1999). Il existe divers critères pour fixer le nombre de classes, ou de partitions, à construire pour bien représenter le jeu de données. L'indice du pseudo-t2 et le critère de classification cubique sont deux cas
particuliers de critères permettant de déterminer le nombre de classes à considérer (CHARRAD et coll., 2012). La classification hiérarchique consiste à emboîter différentes partitions d'objets à classer de façon ordonnée. Le premier niveau d'emboîtement est constitué de n partitions d'un seul objet et le dernier niveau d'emboîtement présente une seule partition de n objets. La classification hiérarchique s'avère utile lorsqu'on désire classer des observations en groupes puis en sous-groupes. Par exemple, en biologie, les familles
4
animales sont divisées en genres animaux qui sont eux-mêmes divisés en espèces. La hiérarchisation des objets à classer est effectuée à l'aide d'algorithmes. À chaque étape de ces algorithmes, on regroupe les classes d'objets les plus similaires ou les moins distantes. Les méthodes algorithmiques se différencient les unes des autres par la façon de calculer les distances ou les similarités entre les classes d'objets après chaque exécution d'une étape de l'algorithme. Par exemple, la méthode du plus proche voisin définit la distance, ou la similarité, entre deux classes comme étant la distance minimale, ou la similarité maximale, entre un objet du premier groupe et un objet du deuxième groupe (GORDON, 1999). Le choix du nombre de classes à retenir en classification hiérarchique peut être effectué en considérant les mêmes critères que ceux utilisés en classification non hiérarchique.
Un autre type de classification est la classification bayésienne. Elle se base sur le théorème de Bayes. En effet, dans ce type de classification, on calcule la probabilité d'un objet non classé jusqu’à maintenant d'appartenir à une classe en sachant l'ensemble des caractéristiques de cet objet. Pour ce faire, il faut considérer la probabilité de posséder les caractéristiques en sachant l'appartenance à la classe
et considérer la probabilité d'appartenir à la classe (GORUNESCU, 2011).
( ) ( ) ( )
∑ ( ) ( ) ( ) ( ) ( ) Les k classes doivent être connues avant le début de la procédure de classification. Les probabilités au numérateur de la formule I.2 sont calculées à l'aide d'un échantillon d'entraînement préalablement choisi. Les probabilités ( ) sont égales à la proportion d'observations appartenant à la classe . La probabilité ( ) suppose l'indépendance entre les éléments de l'ensemble de caractéristiques . On obtient donc l'égalité suivante (GORUNESCU, 2011).
( ) ( ) ( ) ( ) ( ) Si la caractéristique est catégorique, la probabilité ( | ) est la proportion d'objets dans l’échantillon d’entraînement ayant la caractéristique dans la classe . Dans le cas où la caractéristique est quantitative, on suppose que les valeurs que peut prendre cette caractéristique sont distribuées selon une loi de probabilité connue. Habituellement, la loi normale est utilisée lorsqu'il n'y a aucune connaissance a priori sur la distribution des valeurs de la caractéristique. Après avoir calculé les probabilités d'un objet non classé d'appartenir à chacune des k classes, il suffit de classer cet objet dans le groupe dont la probabilité ( ) est maximale (GORUNESCU, 2011).
Le groupement des trente équipes de la Ligue nationale de hockey en six divisions de cinq équipes est avant tout un problème de partitionnement avec contrainte. En effet, on désire obtenir les six classes disjointes minimisant la variance intragroupe sous la condition où chaque classe doit contenir cinq objets. Une approche de classification hiérarchique avec contrainte pourrait aussi être utilisée. Comme il a été mentionné précédemment, les équipes de la Ligue nationale de hockey sont divisées en deux conférences étant elles-mêmes divisées en trois divisions. Il pourrait donc être envisageable de trouver d'abord deux conférences de quinze équipes, puis trois divisions de cinq équipes dans chaque conférence. En fait, la hiérarchie sera obtenue en effectuant deux partitionnements successifs avec contrainte plutôt qu'en utilisant les méthodes classiques de construction de classes de la classification hiérarchique. En effet, les algorithmes de classification hiérarchique ne proposent pas nécessairement des classes de même cardinal.
Dans les chapitres 4, 5 et 7, on présentera trois méthodes développées pour partitionner n objets en
c classes de taille égale. La première approche, développée dans le chapitre 4, consiste à diviser le problème
de partitionnement en plusieurs sous-problèmes, et ce, selon la valeur des variables d'intérêt. La deuxième méthode, décrite au chapitre 5, utilise la même stratégie de subdivision d'un problème global en plusieurs plus petits problèmes, mais selon un critère probabiliste. Enfin, la troisième technique se base sur une chaîne de Markov pour obtenir les partitions optimales. Cette technique est présentée au chapitre 7. Certaines notions reliées aux chaînes de Markov sont définies au chapitre 6. Deux critères d'optimisation seront plus particulièrement utilisés pour déterminer la répartition des objets à classer dans les regroupements à former. Un premier critère de partitionnement consistera à minimiser la variance intraclasse dans le cas où les variables d'intérêt dans la classification sont quantitatives. Si au moins une variable d'intérêt est catégorique, le critère de partitionnement sera la maximisation d'un indice de similarité. Dans le document, les expressions « indice de similitude » et « indice de similarité » seront utilisées de façon équivalente. Les deux critères d’optimisation sont définis au chapitre 1. Le chapitre 2 présente le jeu de données décrivant la position géographique des trente équipes de la Ligue nationale de hockey. Dans le cas où le partitionnement s’effectue avec une seule variable d’intérêt, il est très facile de trouver le regroupement optimal des objets à classer, et ce, peu importe la taille de la population que l’on partitionne. Le cas particulier d’un partitionnement basé sur une seule variable est examiné au chapitre 3. Le chapitre 8 présente une étude de simulations permettant de comparer l’efficacité des trois approches de partitionnement développées dans ce document.
Un long travail de programmation a été nécessaire avant la rédaction du présent mémoire. En effet, chacune des trois nouvelles méthodes de classification a été programmée dans le logiciel R. Les programmes associés à ces trois approches ne sont toutefois pas présentés dans ce mémoire. Ceux-ci sont cependant accessibles sur demande.
1. Définition des critères d'optimisation
Dans le présent document, le partitionnement des individus est basé sur deux principaux critères d'optimisation. Si les variables d'intérêt sont toutes numériques, le partitionnement à obtenir est celui qui minimise la variance intragroupe. Cette variance correspond à la trace de la matrice définie à la formule 1.1.
( ̅)( ̅) ̅ ̅ ( ) La matrice contient la valeur de chaque variable d'intérêt standardisée pour l'ensemble des individus à classer. Elle est composée de n lignes et de p colonnes, où p est le nombre de variables d'intérêt utilisées pour effectuer la classification. La standardisation des valeurs des variables d’intérêt est effectuée pour que chaque variable ait le même « poids » lors de la minimisation de la variance intraclasse. En fait, si la variance d’une des variables d’intérêt est très grande par rapport à la variance des autres variables, la minimisation du critère d’optimisation se fera presque exclusivement par rapport à cette variable. La matrice ̅ est composée de c lignes et de p colonnes. Elle permet d'exprimer sous forme matricielle les moyennes des p variables pour chacune des c classes. La matrice est une matrice de fonctions indicatrices de dimension n par c où l'élément en position (i, j) est égal à un si la ie observation est incluse dans le je groupe. Sinon, cet
élément est égal à zéro (SAS INSTITUTE INC., 1983).
Un autre critère d'optimisation doit être utilisé si les variables d'intérêt sont catégoriques. En fait, le partitionnement défini comme étant optimal dans ce cas est celui qui maximise la somme des similitudes entre tous les individus d'une même classe. La similitude entre le ie et le je objet d'une même partition peut
s'exprimer à l’aide de la formule 1.2.
∑
( )
La quantité est égale à un si la valeur de la le variable est la même pour le ie et le je individus.
Dans le cas contraire, la similitude est nulle (EVERITT, 2011).
Il est possible que certaines variables utilisées pour la classification soient catégoriques et que d'autres variables d'intérêt soient quantitatives. Lorsque cette éventualité se présente, il faut se définir un autre indice de similarité. Une façon d'y arriver est de standardiser les variables numériques. On calcule ensuite une
8
certaine mesure de distance entre la ie et la je observations à classer. Par exemple, la distance 1, qui se
définit par l’expression 1.3, peut être utilisée (DUCHESNE, 2009).
‖ ‖ ∑| |
( )
Il est à noter que est le vecteur des p variables standardisées mesurées sur la ie observation. Le
vecteur est défini de la même façon pour le je individu. La distance entre les deux individus est exprimée
sous la forme d'un indice de similarité, tel que défini par la formule 1.4 (DUSCHESNE, 2009).
‖ ‖ ( )
On calcule ensuite l'indice de similarité 1.2 pour les variables catégoriques. Enfin, l'indice de similarité mixte peut être obtenu en pondérant les indices 1.2 et 1.4 selon le nombre de variables continues, ,
et le nombre de variables catégoriques, , dans le jeu de données. Cette pondération est définie
par la formule 1.5. Le regroupement optimal des individus est celui qui maximise la somme des similitudes entre les objets d'un même groupe.
( )
Dans le cas où les variables d'intérêt sont numériques, il peut être envisageable de vouloir obtenir le partitionnement du point de vue de la maximisation de l'indice de similarité 1.4 plutôt que du point de vue de la minimisation de la trace de la matrice .
2. Présentation du jeu de données
Les méthodes de partitionnement présentées dans ce document sont développées pour trouver le réarrangement optimal des divisions de la Ligue nationale de hockey. Ainsi, avant de présenter les nouvelles approches de partitionnement, il est possible de se familiariser avec le jeu de données utilisé lors des procédures de classification. Étant donné qu'il y a trente équipes dans la Ligue nationale de hockey, le jeu de données contient trente observations correspondant à chacune des villes possédant une équipe dans cette ligue. Le choix du réarrangement optimal des équipes en six divisions de cinq équipes sera fondé sur la valeur de quatre variables géographiques d'intérêt. Deux de ces variables sont quantitatives continues. Ces deux variables correspondent aux coordonnées géographiques longitudinales et latitudinales des villes possédant une équipe de la Ligue nationale de hockey sur leur territoire. Dans le jeu de données, la latitude et la longitude des villes sont exprimées à l'aide de degrés décimaux plutôt qu'avec le système usuel utilisant des degrés, des minutes et des secondes. Les deux autres variables d'intérêt sont qualitatives nominales. Il s'agit en fait du pays et de la province ou de l'état où se trouve chaque équipe. Les valeurs des quatre variables d'intérêt ont été obtenues à l'aide du logiciel Google Earth.
Comme il a été mentionné dans le chapitre précédent, le calcul de la variance intraclasse et de l'indice de similarité est effectué après avoir standardisé les variables quantitatives continues. Ainsi, le jeu de données utilisé lors de la classification doit contenir les valeurs standardisées des coordonnées géographiques des trente villes possédant une équipe de la Ligue nationale de hockey. Le tableau 2.1 présente le jeu de données contenant les variables standardisées. Ces données sont celles utilisées pour illustrer le fonctionnement des trois méthodes de partitionnement développées dans les chapitres 4, 5 et 7.
10
Ville Latitude Longitude Pays Province / État Anaheim 5,358183169 -6,94523634 États-Unis Californie
Boston 6,714571334 -4,18695242 États-Unis Massachusetts Buffalo 6,795178704 -4,64735669 États-Unis New York
Calgary 8,088821426 -6,71990854 Canada Alberta
Caroline 5,6744099 -4,6382711 États-Unis Caroline du Nord Chicago 6,637681778 -5,16573322 États-Unis Illinois Colorado 6,299658969 -6,18698922 États-Unis Colorado
Columbus 6,334665189 -4,89070278 États-Unis Ohio
Dallas 5,196897109 -5,70403739 États-Unis Texas Detroit 6,70812372 -4,89342339 États-Unis Michigan
Edmonton 8,490552335 -6,68474392 Canada Alberta
Floride 4,145984792 -4,73452029 États-Unis Floride Los Angeles 5,395432312 -6,96825614 États-Unis Californie
Minnesota 7,123091873 -5,48547952 États-Unis Minnesota
Montréal 7,210638011 -4,33471009 Canada Québec
Nashville 5,730935319 -5,11296787 États-Unis Tennessee New Jersey 6,45581461 -4,37008901 États-Unis New Jersey New York (Islanders) 6,454122908 -4,33594092 États-Unis New York
New York (Rangers) 6,458399076 -4,35963135 États-Unis New York
Ottawa 7,179076055 -4,47354756 Canada Ontario
Philadelphie 6,324352684 -4,4291346 États-Unis Pennsylvanie Phoenix 5,314356134 -6,61441343 États-Unis Arizona Pittsburgh 6,418590825 -4,71291827 États-Unis Pennsylvanie
San Jose 5,916787828 -7,18238425 États-Unis Californie St. Louis 6,121789664 -5,31468154 États-Unis Missouri Tampa Bay 4,428591599 -4,85803293 États-Unis Floride
Toronto 6,91700376 -4,67699088 Canada Ontario
Vancouver 7,80992435 -7,25349095 Canada Colombie-Britannique Washington 6,164801435 -4,53805666 États-Unis District de Columbia
Winnipeg 7,907515148 -5,72367885 Canada Manitoba
Tableau 2.1 - Jeu de données contenant les variables d'intérêt pour le réarrangement des divisions de la Ligue nationale de hockey
3. Examen du cas du partitionnement à une seule
variable d'intérêt
On peut considérer d'emblée la situation où le regroupement d'objets s'effectue avec une seule variable d'intérêt. Dans ce cas, la classification est évidente. Considérons l'éventualité que cette seule variable d'intérêt soit continue. Lorsque cette situation se produit, seulement une partition d'objets peut former un regroupement optimal. Plus particulièrement, si l'on ordonne les objets selon la valeur de cette unique variable, seuls les regroupements incluant des classes connexes doivent être considérés. Autrement dit, si les éléments i, j et k suivent la relation d'ordre i < j < k et si les éléments i et k appartiennent à une même classe, l'élément j doit aussi appartenir à cette même classe (FISHER, 1958). Ainsi, pour créer c classes optimales de
k objets, il suffit d'ordonner en ordre croissant les individus selon la valeur de la variable d'intérêt. Les k
individus ayant les plus petites valeurs de la variable constituent le premier groupe. Le deuxième groupe contient les individus dont les valeurs de la variable sont situées entre le (k + 1)e et le 2ke rang, et ainsi de
suite. Plus généralement, la ie classe inclut les individus entre le [(i - 1)k + 1]e rang et le ike rang si on les
ordonne selon la valeur de la variable d'intérêt. Par exemple, si l’on considère seulement la variable « Latitude » du jeu de données sur les équipes de la Ligue nationale de hockey, on obtient le réarrangement optimal des divisions présenté dans le tableau 3.1.
Division 1 Division 2 Division 3 Division 4 Division 5 Division 6
Anaheim Boston Calgary Caroline Chicago Colorado
Dallas Buffalo Edmonton Los Angeles Detroit Columbus
Floride Minnesota Montréal Nashville New Jersey Philadelphie Phoenix Ottawa Vancouver San Jose New York (Islanders) Pittsburgh Tampa Bay Toronto Winnipeg St. Louis New York (Rangers) Washington Tableau 3.1 - Réarrangement optimal des divisions de la Ligue nationale de hockey avec « Latitude » comme
seule variable d’intérêt
Dans le cas où la classification s'effectue à l'aide d'une seule variable quantitative discrète, il peut exister plusieurs combinaisons de groupes dont la variance intraclasse est minimale. Ceci est dû au fait que la seule variable d’intérêt peut posséder la même valeur pour plus d’une observation à classer. Si cette situation d’égalité survient, il est relativement facile de trouver au moins un partitionnement minimisant la variance intraclasse. De même, puisque plusieurs objets peuvent appartenir à une même catégorie, des partitionnements différents peuvent maximiser l'indice de similitude lorsque la seule variable d’intérêt est catégorique. Cependant, dans ce dernier cas, ces combinaisons peuvent être formées facilement en regroupant ensemble le plus d’individus appartenant à une même catégorie. Prenons par exemple le cas où
12
l’on voudrait réorganiser les divisions de la Ligue nationale de hockey avec le pays comme seule variable d’intérêt. Une des nombreuses façons d’y arriver est celle présentée dans le tableau 3.2.
Division 1 Division 2 Division 3 Division 4 Division 5 Division 6
Anaheim Boston Buffalo Calgary Chicago Nashville
Minnesota Colorado Caroline Edmonton Columbus New Jersey
Montréal Floride Dallas Ottawa Los Angeles New York (Rangers)
St. Louis Pittsburgh Detroit Vancouver Philadelphie Phoenix
Toronto Tampa Bay New York (Islanders) Winnipeg Washington San Jose Tableau 3.2 - Un des réarrangements optimaux des divisions de la Ligue nationale de hockey avec « Pays »
comme la seule variable d’intérêt
En présence d’un grand nombre d’individus ou d’un grand nombre de catégories distinctes, il peut devenir difficile de trouver un partitionnement optimal. Il en est de même dans le cas d'une variable quantitative discrète dont les valeurs proviennent d’un ensemble relativement petit. En effet, dans ces circonstances, il peut exister un très grand nombre de regroupements optimaux. Il peut donc être pertinent d'utiliser l’une des trois méthodes présentées dans les chapitres 4, 5 et 7 pour découvrir certains de ces regroupements optimaux.
4. Présentation de l'approche algorithmique
Si le jeu de données utilisé pour la classification contient plus d'une variable d'intérêt, il devient difficile à partir d'un certain nombre d'individus de trouver le regroupement optimal d'objets en plusieurs groupes ayant le même cardinal. Cependant, pour une petite quantité d'objets à classer, il est envisageable de considérer l'ensemble des regroupements potentiels. Il est donc possible, dans ce cas, de trouver la combinaison de groupes maximisant la similitude intragroupe ou minimisant la variance intragroupe. Ainsi, une approche intéressante à considérer est de diviser notre population d'individus à classer en plusieurs sous-populations d'individus lorsque le nombre d'objets à classer est trop élevé pour que les logiciels actuels, tels que R, soient capables d'obtenir toutes les possibilités de regroupements.
Deux conditions doivent être remplies pour que cette méthode de partitionnement algorithmique fonctionne. Il faut, entre autres, que la taille des sous-populations soit petite. Dans le cas contraire, il sera impossible d'obtenir rapidement l'ensemble des partitionnements possibles. Pour savoir si la taille de la population est assez petite pour trouver l'ensemble des partitionnements imaginables dans cette sous-population, on peut utiliser la fonction setparts du logiciel R (HANKIN et WEST, 2007). En fait, si le résultat de la fonction est un message d’erreur, la taille de cette population est trop grande. La taille des sous-populations doit également être un multiple strictement positif de k, qui est la taille des c classes à former. Cette dernière condition doit être remplie pour qu'il soit possible de créer des classes de taille k dans les sous-populations.
La division des individus en plus petites sous-populations peut s'effectuer en considérant les valeurs prises par les objets à classer pour chaque variable d'intérêt. Si les variables utilisées pour la classification sont numériques, on peut mettre les objets en ordre croissant selon la valeur d'une première variable. On crée ensuite, selon l'ordre pris par les objets, des sous-populations qui réuniront des objets contigus. La taille de ces sous-populations devra être relativement petite. En effet, pour cette première variable, on doit obtenir les regroupements optimaux des objets à l'intérieur de chacune des sous-populations. Ces regroupements basés sur toutes les variables du jeu de données seront obtenus en considérant l'ensemble des partitions de taille k qu'il est possible de former dans chacun des sous-groupes. La réunion des partitions optimales obtenues dans chaque sous-population devient un regroupement à considérer pour l'ensemble de la population. Après avoir effectué ces étapes pour une variable, on fait de même pour les autres variables. On obtient donc un regroupement pour chacune des variables. On compare ensuite l'ensemble des regroupements obtenus. On conserve celui pour lequel la variance intraclasse est minimale.
14
Si l'on est plutôt en présence de variables catégoriques, on sépare également la population en plusieurs sous-populations. Puisqu'il n'y a pas nécessairement une relation d'ordre entre les catégories, il suffit de former les sous-populations en essayant d'inclure dans les sous-groupes le plus d'individus appartenant à la même catégorie selon une première variable. En d'autres mots, il faut trouver les sous-populations maximisant la similitude intraclasse sous les contraintes du nombre et de la taille des sous-populations que l'on désire créer. Ensuite, tout comme dans le cas de variables continues, on considère l'ensemble des façons de former des classes de taille k dans chaque sous-population pour trouver le partitionnement optimal basé sur toutes les variables d'intérêt. Ces regroupements optimaux ainsi obtenus dans les sous-populations suggèrent une première façon de partitionner l'ensemble des individus du jeu de données. En répétant ces étapes pour les autres variables catégoriques d'intérêt, on obtient plusieurs possibilités de regroupements de la population en c classes de taille k. Il suffit ensuite de comparer les indices de similitude de toutes ces possibilités pour trouver le partitionnement à conserver.
Comme il a été mentionné au précédent chapitre, lorsqu’on considère une seule variable catégorique ou une seule variable quantitative discrète, plusieurs partitionnements optimaux peuvent être formés. Ainsi, lors de l'exécution de la méthode algorithmique, il se peut qu'il y ait un très grand nombre de manières de créer les sous-populations qui optimisent la similitude ou la variance intraclasse pour une certaine variable. Le cas échéant, il est impossible de considérer l'ensemble des combinaisons de sous-populations optimisant la valeur des critères du deuxième chapitre. Ainsi, lorsque la variable est catégorique, il vaut mieux ne pas utiliser l'approche algorithmique pour économiser du temps. Si la variable est de type quantitatif ou de type catégorique ordinal, la multiplicité des partitionnements optimaux est due à une égalité de la valeur d’une variable d’intérêt entre des observations pouvant être placées dans des classes différentes. Dans ce cas, on peut trier les observations à classer selon cette variable, puis selon une deuxième variable quantitative ou catégorique ordinale. On formera ensuite les sous-populations en considérant l'ordre obtenu lors de ce tri. Dans l'éventualité où des observations ayant la même valeur pour ces deux variables devaient encore une fois être séparées dans des sous-populations différentes, on peut effectuer le tri jusqu'à ce qu'il n'y ait plus d'égalité. Le choix de la deuxième variable est arbitraire. Cependant, il est possible d'utiliser toutes les autres variables continues ou catégoriques ordinales. On peut ensuite comparer les critères d'optimalisation pour l'ensemble des tris possibles.
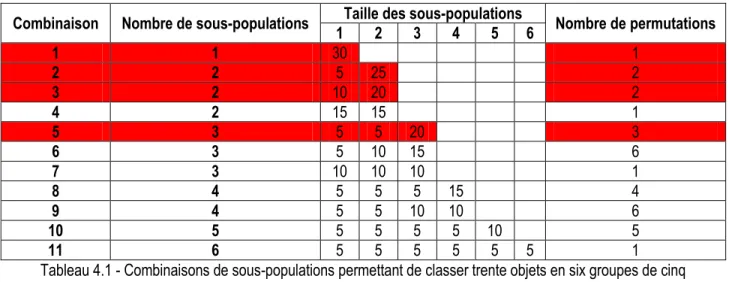
Il peut exister une multitude de façons de diviser la population d'objets à classer en plusieurs sous-populations. Le tableau 4.1 montre la taille de plusieurs combinaisons de sous-populations qu'il est possible de former à partir d'une population de trente individus. Ces combinaisons permettent de créer six groupes de cinq objets, tout comme dans le cas de la réorganisation des divisions de la Ligue nationale de hockey.
Combinaison Nombre de sous-populations 1 Taille des sous-populations 2 3 4 5 6 Nombre de permutations 1 1 30 1 2 2 5 25 2 3 2 10 20 2 4 2 15 15 1 5 3 5 5 20 3 6 3 5 10 15 6 7 3 10 10 10 1 8 4 5 5 5 15 4 9 4 5 5 10 10 6 10 5 5 5 5 5 10 5 11 6 5 5 5 5 5 5 1
Tableau 4.1 - Combinaisons de sous-populations permettant de classer trente objets en six groupes de cinq objets
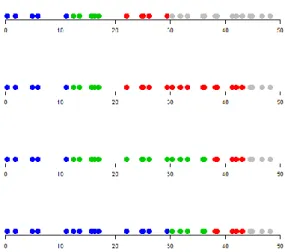
Certaines combinaisons contiennent des sous-populations pour lesquelles la taille est encore trop grande pour être capable d'obtenir l'ensemble des possibilités de former des groupes de cinq objets dans la sous-population. C'est le cas des première, deuxième, troisième et cinquième combinaisons qui sont surlignées en rouge dans le tableau 4.1. Il reste donc sept façons de diviser la population en plus petites sous-populations. Ces combinaisons incluent d'une à six permutations de la taille des sous-sous-populations. Par exemple, pour bien illustrer ce concept de permutations de la taille des sous-populations, observons la huitième combinaison dans le cas d'une variable d'intérêt continue. Comme le montre la figure 4.1, il existe quatre façons de créer trois groupes de cinq individus et un groupe de quinze individus dans une population de trente individus. Les quatre axes de cette figure correspondent à l’une des quatre façons de créer trois groupes de cinq objets et un groupe de quinze objets. Les points de la même couleur sur un même axe sont inclus dans la même sous-population. Ainsi, comme on peut le voir sur l’axe supérieur de la figure 4.1, la première permutation divise la population en trois groupes de cinq individus et en un groupe de quinze individus. On note cette permutation {5, 5, 5, 15}. La première sous-population inclut les cinq plus petites valeurs d’une des variables d’intérêt. Ce sous-groupe est représenté par les cinq points bleus sur l’axe supérieur de la figure. De même, les points verts situés sur ce même axe correspondent aux valeurs de la même variable d’intérêt pour les cinq individus d’un deuxième sous-groupe. Les points rouges identifient les valeurs de la variable d’intérêt des individus appartenant à une troisième sous-population. Enfin, les quinze autres individus de la population sont placés dans la sous-population comptant quinze objets. Ceux-ci sont représentés en gris sur l’axe supérieur de la figure 4.1. Ces quinze individus appartiennent à la même sous-population, car ils sont ceux qui possèdent les quinze plus grandes valeurs de la variable d’intérêt en question. De la même façon, la figure 4.1 illustre la formation des trois autres permutations associées à la huitième combinaison de sous-population du tableau 4.1. Ces permutations sont dénotées {5, 5, 15, 5}, {5, 15, 5, 5} et {15, 5, 5, 5}. Elles sont respectivement illustrées par les deuxième, troisième et quatrième axes de la figure.
16
Figure 4.1 - Permutations possibles de la taille des sous-populations dans le cas de la huitième combinaison du tableau 4.1
Le choix de la combinaison à retenir pour la formation de sous-groupes est laissé à l'expérimentateur. On peut cependant considérer l'ensemble des combinaisons de sous-populations pour chacune des variables. En effet, ceci permet d'explorer une plus grande variété de manières de diviser la population en c groupes de
k individus. Il y a donc plus de chances de trouver le regroupement optimal des n objets à classer. Cependant,
dans certaines circonstances, il est possible qu'il y ait un grand nombre de combinaisons ou de permutations à l'intérieur des combinaisons que l'on peut utiliser lors de l'exécution de l'approche algorithmique. Dans ce cas, plutôt que de considérer l'ensemble de ces combinaisons ou de ces permutations, il peut être pertinent d'en sélectionner seulement quelques-unes ou de ne pas utiliser l’approche algorithmique. Pour bien comprendre la méthode présentée dans ce chapitre, il peut être utile de résumer chacune des étapes de l'algorithme proposé.
1. Choix du nombre de classes à créer dans la population;
2. Choix du critère d'optimalisation selon la nature des variables d'intérêt; 3. Obtention de l'ensemble des combinaisons de tailles de sous-populations;
4. Élimination des combinaisons contenant des tailles de sous-populations trop grandes; 5. Considération d'une combinaison restante de tailles de sous-population;
6. Obtention des permutations de tailles de sous-populations pour cette combinaison; 7. Considération d'une permutation de tailles de sous-population pour cette combinaison;
8. Séparation de la population en plusieurs sous-populations optimales selon les valeurs d'une variable d'intérêt;
a. Cas d'une variable quantitative continue : Utilisation de la méthode de partitionnement de Fisher présentée au chapitre 3 pour créer les sous-populations;
b. Cas d'une variable quantitative discrète ou d'une variable catégorique ordinale : Création des sous-populations avec la méthode de partitionnement de Fisher et traitement des égalités avec d'autres variables;
c. Cas d'une variable catégorique nominale : Considération de l'unique partitionnement optimal de la population en sous-population ou abandon de la procédure de séparation pour cette variable.
9. Obtention des partitionnements optimaux à l'intérieur de chaque sous-population en considérant toutes les variables d'intérêt et calcul du critère d'optimalisation;
10. Addition des critères d'optimalisation de chaque sous-population pour obtenir une valeur globale du critère d'optimalisation pour toute la population;
11. Répétition des étapes huit à dix pour toutes les variables d'intérêt;
12. Répétition des étapes sept à onze pour toutes les permutations de tailles de sous-population de la combinaison;
13. Répétition des étapes cinq à douze pour toutes les combinaisons de tailles de sous-population; 14. Comparaison de l'ensemble des valeurs des critères d'optimalisation obtenues et rétention du
partitionnement optimisant le critère retenu.
Il est maintenant possible d’utiliser l’algorithme ci-dessus pour tenter de trouver la façon optimale de classer les trente équipes de la Ligue nationale de hockey en six divisions de cinq équipes. Pour ce faire, utilisons le jeu de données présenté au chapitre 2. Ce jeu de données contient à la fois des variables quantitatives et des variables qualitatives. Il faudra donc utiliser la maximisation d’un indice de similitude comme critère d’optimisation.
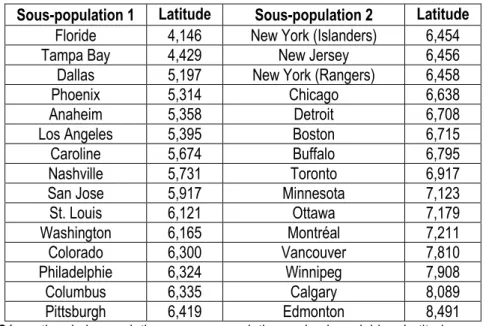
Toutes les combinaisons de tailles de sous-populations qu’il est possible de créer sont présentées dans le tableau 4.1. Ce tableau présente également l'ensemble des combinaisons qu'il sera impossible de considérer en raison de la trop grande taille de certaines sous-populations. La quatrième combinaison, qui sépare la population à classer en deux groupes de quinze individus, est la première combinaison à analyser. Cette combinaison ne possède qu'une seule permutation de la taille des sous-populations. Il faut maintenant séparer la population en sous-populations selon une première variable d'intérêt. Considérons la variable « Latitude ». En ordonnant les observations du jeu de données selon cette première variable, on obtient les deux sous-populations du tableau 4.2.
Sous-population 1 Latitude Sous-population 2 Latitude
Floride 4,146 New York (Islanders) 6,454
Tampa Bay 4,429 New Jersey 6,456
Dallas 5,197 New York (Rangers) 6,458
Phoenix 5,314 Chicago 6,638
Anaheim 5,358 Detroit 6,708
Los Angeles 5,395 Boston 6,715
Caroline 5,674 Buffalo 6,795
Nashville 5,731 Toronto 6,917
San Jose 5,917 Minnesota 7,123
St. Louis 6,121 Ottawa 7,179 Washington 6,165 Montréal 7,211 Colorado 6,300 Vancouver 7,810 Philadelphie 6,324 Winnipeg 7,908 Columbus 6,335 Calgary 8,089 Pittsburgh 6,419 Edmonton 8,491
Tableau 4.2 - Séparation de la population en sous-populations selon la variable « Latitude » pour la quatrième combinaison du tableau 4.1
18
On peut obtenir les partitionnements optimaux à l'intérieur de ces deux sous-populations. Ces partitionnements sont basés sur les quatre variables d'intérêt du jeu de données. Le tableau 4.3 résume les résultats obtenus lors de cette première classification. L'indice de similarité s'élève à 49,004 pour la première sous-population et à 46,641 pour la deuxième sous-population. On obtient ainsi un indice de similarité global de 95,645. On peut maintenant créer deux sous-populations de quinze observations selon une deuxième variable d'intérêt, soit la longitude des villes possédant une équipe de la Ligue nationale de hockey. Ces sous-populations sont présentées dans le tableau 4.4.
Sous-population 1 Sous-population 2
Division 1 Division 2 Division 3 Division 4 Division 5 Division 6
Anaheim Caroline Columbus Boston Calgary Chicago
Colorado Dallas Philadelphie Buffalo Edmonton Detroit
Los Angeles Floride Pittsburgh New Jersey Montréal Minnesota Phoenix Nashville St. Louis New York (Islanders) Vancouver Ottawa San Jose Tampa Bay Washington New York (Rangers) Winnipeg Toronto Tableau 4.3 - Divisions optimales obtenues lors de la séparation de la population en sous-populations selon la
variable « Latitude » pour la quatrième combinaison du tableau 4.1 Sous-population 1 Longitude Sous-population 2 Longitude
Vancouver -7,253 Columbus -4,891
San Jose -7,182 Tampa Bay -4,858
Los Angeles -6,968 Floride -4,735
Anaheim -6,945 Pittsburgh -4,713 Calgary -6,720 Toronto -4,677 Edmonton -6,685 Buffalo -4,647 Phoenix -6,614 Caroline -4,638 Colorado -6,187 Washington -4,538 Winnipeg -5,724 Ottawa -4,474 Dallas -5,704 Philadelphie -4,429
Minnesota -5,485 New Jersey -4,370
St. Louis -5,315 New York (Rangers) -4,360 Chicago -5,166 New York (Islanders) -4,336
Nashville -5,113 Montréal -4,335
Detroit -4,893 Boston -4,187
Tableau 4.4 - Séparation de la population en sous-populations selon la variable « Longitude » pour la quatrième combinaison du tableau 4.1
Sous-population 1 Sous-population 2
Division 1 Division 2 Division 3 Division 4 Division 5 Division 6
Calgary Anaheim Chicago Caroline New Jersey Boston
Colorado Dallas Detroit Columbus New York (Islanders) Buffalo Edmonton Los Angeles Minnesota Floride New York (Rangers) Montréal Vancouver Phoenix Nashville Tampa Bay Philadelphie Ottawa
Winnipeg San Jose St. Louis Washington Pittsburgh Toronto Tableau 4.5 - Divisions optimales obtenues lors de la séparation de la population en sous-populations selon la
Le tableau 4.5 présente les divisions proposées par les regroupements optimaux à l'intérieur des deux populations créées selon les valeurs de la variable « Longitude ». Pour la première sous-population, l'indice de similarité est de 45,003. L'indice de similarité dans la deuxième sous-population est égal à 48,530. On obtient donc un indice de similarité global de 93,533.
Après avoir partitionné la population d'objets à classer selon les valeurs des deux variables quantitatives du jeu de données, il faudrait maintenant faire de même pour les deux variables catégoriques. Cependant, il existe un très grand nombre d'arrangements de sous-populations qui maximisent la similitude lorsqu'une seule de ces deux variables est prise en compte. Ainsi, il est impossible d'utiliser l'approche algorithmique pour les deux variables qualitatives nominales.
Combinaison Permutation Variable Indice de similitude Variable Indice de similitude
4 {15, 15} Latitude 95,645 Longitude 93,533 6 {5, 10, 15} Latitude 92,886 Longitude 86,825 6 {5, 15, 10} Latitude 91,985 Longitude 85,789 6 {10, 5, 15} Latitude 95,183 Longitude 93,533 6 {10, 15, 5} Latitude 95,183 Longitude 91,247 6 {15, 5, 10} Latitude 94,092 Longitude 89,599 6 {15, 10, 5} Latitude 95,645 Longitude 90,372 7 {10, 10, 10} Latitude 94,539 Longitude 90,362 8 {5, 5, 5, 15} Latitude 92,186 Longitude 86,825 8 {5, 5, 15, 5} Latitude 92,186 Longitude 84,539 8 {5, 15, 5, 5} Latitude 91,985 Longitude 83,643 8 {15, 5, 5, 5} Latitude 94,092 Longitude 87,453 9 {5, 5, 10, 10} Latitude 91,542 Longitude 83,654 9 {5, 10, 5, 10} Latitude 91,333 Longitude 82,890 9 {5, 10, 10, 5} Latitude 92,886 Longitude 83,663 9 {10, 5, 5, 10} Latitude 93,630 Longitude 89,599 9 {10, 5, 10, 5} Latitude 95,183 Longitude 90,372 9 {10, 10, 5, 5} Latitude 94,539 Longitude 88,217 10 {5, 5, 5, 5, 10} Latitude 90,633 Longitude 82,890 10 {5, 5, 5, 10, 5} Latitude 92,186 Longitude 83,663 10 {5, 5, 10, 5, 5} Latitude 91,542 Longitude 81,509 10 {5, 10, 5, 5, 5} Latitude 91,333 Longitude 80,745 10 {10, 5, 5, 5, 5} Latitude 93,630 Longitude 87,453 11 {5, 5, 5, 5, 5, 5} Latitude 90,633 Longitude 80,745
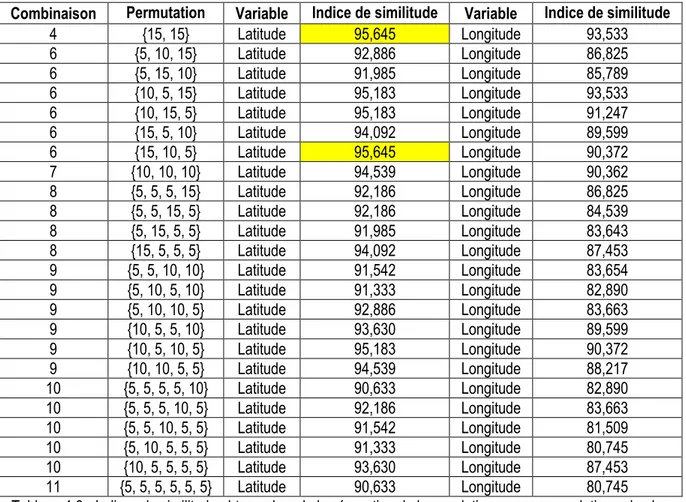
Tableau 4.6 - Indices de similitude obtenus lors de la séparation de la population en sous-population selon les deux variables quantitatives en considérant toutes les combinaisons du tableau 4.1
Jusqu'à maintenant, seuls les partitionnements optimaux basés sur la quatrième combinaison de tailles de sous-populations ont été explorés. Il reste donc encore six combinaisons à considérer. Les indices de similitude obtenus à l'aide de l'ensemble des combinaisons sont présentés dans le tableau 4.6. Comme on peut le voir dans ce tableau, le plus grand indice de similitude observé pour l’ensemble de la procédure algorithmique s’élève à 95,645. Jusqu’à présent, le meilleur regroupement des équipes de la Ligue nationale
20
de hockey en six divisions de cinq équipes est proposé, entre autres, par la quatrième combinaison de tailles de sous-populations qui utilise la variable « Latitude » comme variable de tri. Ces divisions « optimales » sont présentées précédemment dans le tableau 4.3.
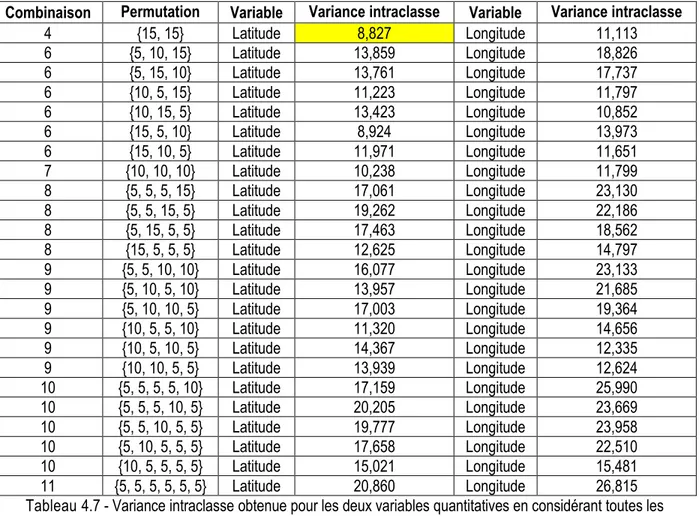
De plus, on pourrait calculer la variance intraclasse de chaque partitionnement proposé par la méthode algorithmique, en ne considérant que les deux variables quantitatives. Le tableau 4.7 présente la variance intraclasse de chaque permutation de tailles de sous-population issue de l'ensemble des combinaisons de tailles de sous-population du tableau 4.1.
Combinaison Permutation Variable Variance intraclasse Variable Variance intraclasse
4 {15, 15} Latitude 8,827 Longitude 11,113 6 {5, 10, 15} Latitude 13,859 Longitude 18,826 6 {5, 15, 10} Latitude 13,761 Longitude 17,737 6 {10, 5, 15} Latitude 11,223 Longitude 11,797 6 {10, 15, 5} Latitude 13,423 Longitude 10,852 6 {15, 5, 10} Latitude 8,924 Longitude 13,973 6 {15, 10, 5} Latitude 11,971 Longitude 11,651 7 {10, 10, 10} Latitude 10,238 Longitude 11,799 8 {5, 5, 5, 15} Latitude 17,061 Longitude 23,130 8 {5, 5, 15, 5} Latitude 19,262 Longitude 22,186 8 {5, 15, 5, 5} Latitude 17,463 Longitude 18,562 8 {15, 5, 5, 5} Latitude 12,625 Longitude 14,797 9 {5, 5, 10, 10} Latitude 16,077 Longitude 23,133 9 {5, 10, 5, 10} Latitude 13,957 Longitude 21,685 9 {5, 10, 10, 5} Latitude 17,003 Longitude 19,364 9 {10, 5, 5, 10} Latitude 11,320 Longitude 14,656 9 {10, 5, 10, 5} Latitude 14,367 Longitude 12,335 9 {10, 10, 5, 5} Latitude 13,939 Longitude 12,624 10 {5, 5, 5, 5, 10} Latitude 17,159 Longitude 25,990 10 {5, 5, 5, 10, 5} Latitude 20,205 Longitude 23,669 10 {5, 5, 10, 5, 5} Latitude 19,777 Longitude 23,958 10 {5, 10, 5, 5, 5} Latitude 17,658 Longitude 22,510 10 {10, 5, 5, 5, 5} Latitude 15,021 Longitude 15,481 11 {5, 5, 5, 5, 5, 5} Latitude 20,860 Longitude 26,815
Tableau 4.7 - Variance intraclasse obtenue pour les deux variables quantitatives en considérant toutes les combinaisons du tableau 4.1
Sous-population 1 Sous-population 2
Division 1 Division 2 Division 3 Division 4 Division 5 Division 6
Anaheim Caroline Columbus Boston Buffalo Calgary
Colorado Dallas Philadelphie Montréal Chicago Edmonton
Los Angeles Floride Pittsburgh New Jersey Detroit Minnesota Phoenix Nashville St. Louis New York (Islanders) Ottawa Vancouver San Jose Tampa Bay Washington New York (Rangers) Toronto Winnipeg Tableau 4.8 - Divisions optimales d’un point de vue de la minimisation de la variance intraclasse obtenues lors
Si l’on considère seulement la longitude et la latitude comme variables d’intérêt, c’est encore une fois avec la quatrième combinaison de tailles de sous-populations que l’on obtient le meilleur partitionnement de la méthode algorithmique. Le regroupement le plus « optimal » proposé par la présente approche est résumé dans le tableau 4.8.
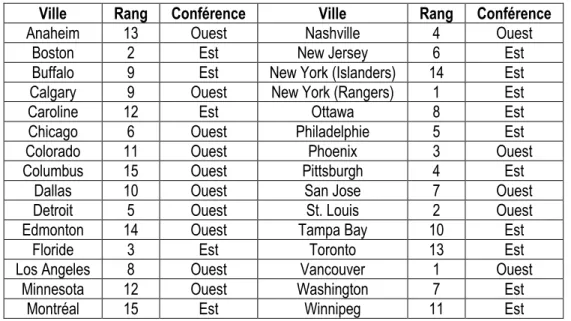
Comme on peut le voir dans cet exemple, la séparation de la population d'objets à classer en sous-populations s'est effectuée exclusivement selon des variables continues. En effet, le jeu de données sur la Ligue nationale de hockey ne contient pas de variables qualitatives ordinales ou de variables quantitatives discrètes. Conséquemment, la procédure de traitement des égalités prévue dans la méthode algorithmique n'a pu être exemplifiée. De plus, les deux variables catégoriques caractérisant les observations à classer ne permettent pas de diviser de façon unique les observations en sous-populations. De cette façon, aucune illustration d'une classification basée sur des variables catégoriques n'a pu être effectuée. Ainsi, pour bien expliciter l'ensemble de la méthode algorithmique, considérons deux nouvelles variables. Les variables « Rang » et « Conférence » contiennent respectivement le classement des équipes dans la conférence dans laquelle elles évoluaient lors de la saison 2011-2012 et le nom de cette conférence (LIGUE NATIONALE DE HOCKEY, 2012). Les valeurs de ces variables sont présentées dans le tableau 4.9.
Ville Rang Conférence Ville Rang Conférence
Anaheim 13 Ouest Nashville 4 Ouest
Boston 2 Est New Jersey 6 Est
Buffalo 9 Est New York (Islanders) 14 Est
Calgary 9 Ouest New York (Rangers) 1 Est
Caroline 12 Est Ottawa 8 Est
Chicago 6 Ouest Philadelphie 5 Est
Colorado 11 Ouest Phoenix 3 Ouest
Columbus 15 Ouest Pittsburgh 4 Est
Dallas 10 Ouest San Jose 7 Ouest
Detroit 5 Ouest St. Louis 2 Ouest
Edmonton 14 Ouest Tampa Bay 10 Est
Floride 3 Est Toronto 13 Est
Los Angeles 8 Ouest Vancouver 1 Ouest
Minnesota 12 Ouest Washington 7 Est
Montréal 15 Est Winnipeg 11 Est
Tableau 4.9 - Jeu de données contenant deux nouvelles variables permettant d'expliciter le traitement des égalités et des variables catégoriques dans la méthode algorithmique
Pour donner un exemple de la façon de traiter les égalités avec une variable ordinale ou discrète, séparons les trente observations en groupes selon la quatrième combinaison de tailles de sous-populations du tableau 4.1. En fait, si l'on ordonne les équipes selon la variable « Rang » pour ensuite former les deux groupes de quinze équipes, on s'aperçoit qu'il faut placer dans deux sous-populations différentes deux observations avec le même rang. Cette situation est illustrée dans le tableau 4.10. Il faut donc utiliser
22
une autre variable, continue de préférence, pour traiter les égalités lors de la création des sous-populations. Effectivement, si la variable est continue, deux observations ne peuvent pas avoir la même valeur pour cette variable. On n’a donc pas besoin d’une autre variable pour traiter les égalités. Dans le présent exemple, considérons la variable « Latitude » comme variable de « bris d'égalité ». Après avoir formé les sous-groupes d'objets à classer, la procédure algorithmique se continue de la même manière qu'avec une variable continue.
Sous-population 1 Rang Latitude Sous-population 2 Rang Latitude
New York (Rangers) 1 6,458 Ottawa 8 7,179
Vancouver 1 7,810 Buffalo 9 6,795
St. Louis 2 6,122 Calgary 9 8,089
Boston 2 6,715 Tampa Bay 10 4,429
Floride 3 4,146 Dallas 10 5,197 Phoenix 3 5,314 Colorado 11 6,300 Nashville 4 5,731 Winnipeg 11 7,908 Pittsburgh 4 6,419 Caroline 12 5,674 Philadelphie 5 6,324 Minnesota 12 7,123 Detroit 5 6,708 Anaheim 13 5,358
New Jersey 6 6,456 Toronto 13 6,917
Chicago 6 6,638 New York (Islanders) 14 6,454
San Jose 7 5,917 Edmonton 14 8,491
Washington 7 6,165 Columbus 15 6,335
Los Angeles 8 5,395 Montréal 15 7,211
Tableau 4.10 - Séparation de la population en sous-populations selon la variable « Rang » considérant la variable « Latitude » comme variable de « bris d'égalité » pour la quatrième combinaison du tableau 4.1
La quatrième combinaison de tailles de sous-populations présentée dans le tableau 4.1 peut aussi être utilisée pour créer des sous-groupes selon la variable « Conférence ». En effet, puisqu'il y a quinze équipes dans la conférence de l'Ouest et quinze équipes dans la conférence de l'Est, il existe une seule façon de classer les trente équipes à classer en deux groupes optimaux selon cette dernière variable catégorique. Ainsi, dans ce cas, il est possible d'effectuer toutes les étapes de l'approche algorithmique basées sur une variable qualitative catégorique.
Comme tout bon algorithme, l'exécution de la méthode de classification algorithmique s'effectue en suivant à la lettre des étapes dans un certain ordre. Cette façon de faire se démarque ainsi par sa simplicité. En effet, si l'on comprend chacune des étapes de l'approche algorithmique, il est relativement facile de bien saisir le fonctionnement de la méthode. Cette technique est aussi très accessible. En fait, seules des connaissances de base en mathématiques et en statistique sont nécessaires pour comprendre et pour utiliser l'algorithme. Donc, tous les expérimentateurs sont quand même en mesure de comprendre la théorie derrière chaque point de l'algorithme. La méthode développée dans ce chapitre réduit une question de partitionnement optimal que l'on est incapable de résoudre en plusieurs sous-questions pouvant être résolues dans un temps raisonnable par un ordinateur moderne. De cette manière, cette approche de classification possède également