Crack inspection and simulations with Eddy Current Thermography for the aerospace industry

(1)

Crack Inspection and simulations with Eddy Current

Thermography for the Aerospace Industry

Mémoire

Gia Phuong Tran

Maîtrise en génie électrique

Maître ès sciences (M.Sc.)

Québec, Canada

(2)

(3)

iii

Résumé

La Thermographie des Courants de Foucault (Eddy Current Thermography, ECT) est une méthode de contrôle non-destructif (CND) sans contact, et de nos jours il est utilisé dans une large gamme d'applications. Cette méthode combine les techniques de courants de Foucault et des techniques de thermographies de type CND afin de fournir une méthode efficace pour la détection des fissures. Dans cette méthode, le courant de Foucault est généré dans les échantillons métalliques. Si l'échantillon contient des fissures, le déplacement du courant et la propagation de la température à l'intérieur des échantillons métalliques seraient affectés par ces fissures. Les changements de la distribution de température sont captés par une caméra infrarouge.

L'un des principaux défis de cette méthode est qu'elle nécessite beaucoup de paramètres dans les expériences, tels que l’excitation des bobines: la valeur de la fréquence, le nombre de tours, le matériel de fil, le rayon de la bobine ... Afin d'optimiser les expériences, la simulation numérique est nécessaire, et le logiciel COMSOL Multiphysics® FEM est une solution très appropriée.

Pendant le processus de simulation, une limite de détection de fissure a été proposée pour une fissure dans un spécimen métallique donné. Les résultats de la simulation et de la limite de détection des fissures sont également vérifiés au moyen d’expériences en laboratoire.

L'objectif final de cette thèse est de fournir une image globale de la Thermographie des Courants de Foucault, la limite de détection des fissures et la manière dont la simulation ainsi que les expériences doivent être effectue afin de détecter les fissures dans les échantillons de plaques métalliques. Ces échantillons ont été fournis par L3-MAS et Pratt & Whitney Canada (PWC), les partenaires industriels impliqués dans ce projet quia été financé par le Conseil de recherches en sciences naturelles et en génie du Canada (CRSNG) et le Consortium de recherche et d'innovation en aérospatiale au Québec (CRIAQ).

(4)

(5)

v

Abstract

Eddy Current Thermography (ECT) is a non-contact, non-destructive testing (NDT) method, and nowadays it is used in a wide range of applications. This method combines eddy current and thermographic NDT techniques in order to provide an efficient method for crack detection. In this method, the eddy current is generated into metallic specimens. If the specimen contains cracks, the current flow and temperature propagation inside the metallic specimens would be affected by these cracks. The changes of temperature distribution are captured by an infrared camera.

One of the main challenges in this method is that it requires many parameters in the experiments, such as coil excitations: the frequency value, number of turns, material of wire, radius of the coil...In order to optimize the experiments, numerical simulation is necessary, and COMSOL Multiphysics®_{FEM software is a very suitable solution.}

During the simulation process, a crack detection limit for a crack in a given metallic specimen has been proposed. The simulation results and crack detection limit are also verified using experiments in the laboratory.

The final goal of this thesis is to provide the overall picture of the Eddy Current Thermography, crack detection limit and the manner in which to simulate as well as perform the experiments in order to detect cracks on the metallic plate specimens which were provided by L3-MAS and Pratt & Whitney Canada (P.W.C), the industrial partners involved in this project which was sponsored by the Natural Sciences and Engineering Research Council of Canada (NSERC) and The Consortium for Research and Innovation in Aerospace in Québec (CRIAQ).

(6)

(7)

vii

Acknowledgment

First of all, I would like to express my deepest gratitude to my supervisor, Professor Xavier Maldague for his invaluable support during my studies at Université Laval. It is truly an honor for me to be one of his students. He gave me many excellent lessons in order to help me to build my knowledge in Electrical Engineering area, and he also encourages me doing many research activities. My master thesis would not have been possible without his amazing support.

I would like to thank my co-supervisor, Professor Lionel Birglen at Polytechnique Montréal for his support and advices during my research project. I also wish to thank all of members in the research project CRIAQ-MANU 418 for their discussions in monthly meeting, in particular, Professor Martin Viens at École de Technologie Supérieure. He spent so much effort to give me many advices for my research results in the monthly meetings.

Special thanks to Marc Grenier, Denis Ouellet of the Computer Vision and Systems Laboratory. They helped me to understand the basic steps in establishing the experiments.

I also would like to thank the Computer and Electrical Engineering Department, Université Laval, and the Canada Research Chair in multipolar infrared vision (MIVIM) for the excellent resources they provided me with a very powerful computer, electrical equipment and devices during my studies and research.

I acknowledge and greatly appreciate the financial support of The Consortium for Research and Innovation in Aerospace in Québec (CRIAQ), and also the Natural Sciences and Engineering Research Council of Canada (NSERC) for the project CRIAQ MANU-418.

Finally, I would like to thank all of my teammates at the Canada Research Chair in Multipolar Infrared Vision (MIVIM), Vietnamese students and international students at Université Laval, who made my 2 years in Quebec City to be one of the best moments in my life.

(8)

(9)

ix

List of Tables

Table 4. 1: The thermal and coil’s excitation parameters for simulations ... 25

Table 5.1: Crack information ... 36

Table 6.1 : Statistic information about cracks ... 42

List of Figures

Figure 2. 1: Experimental setup for active thermography [16]. ... 5

Figure 2. 2 : Schematic configuration of lock-in thermography [6]. ... 6

Figure 2. 3 : Schematic configuration of pulsed thermography [6]. ... 7

Figure 2. 4 : Schematic setup of optical excitation thermography (Reflection mode). ... 9

Figure 3. 1 : Resistive elements in circuit. ... 12

Figure 3. 2 : Induction coil with electromagnetic field [24]. ... 13

Figure 3. 3 : Reference depth for several materials [22] ... 15

Figure 3. 4 : Excitation frequency and magnetic properties [27]. ... 15

Figure 3. 5 : A schematic setup of Eddy Current Thermography for NDT [16]. ... 16

Figure 4. 1 : COMSOL integrated development environment. ... 19

Figure 4. 2 : Settings window... 20

Figure 4. 3 : Preference window. ... 20

Figure 4. 4 : Global Definitions and Results nodes... 21

Figure 4. 5 : Parameters... 21

Figure 4. 6 : Result node. ... 22

Figure 4. 7 : Model and Study nodes. ... 22

Figure 4. 8 : Model Library examples. ... 23

Figure 4. 9 : Workflow and sequence of operations. ... 23

Figure 4. 10 : 2-D simulation of Eddy Current Thermography. ... 26

Figure 4. 11 : Induction heating simulation in 2-D. ... 27

Figure 4. 12 : 3-D simulation of Eddy Current Thermography. ... 28

Figure 4. 13 : Geometry of Induction heating simulations in 3-D. ... 28

Figure 5. 1 : Experiment setup ... 30

Figure 5. 2 : Experimental diagram. ... 31

Figure 5. 3: Infrared Camera in ECT experiment. ... 31

Figure 5. 4: IR camera software. ... 32

Figure 5. 5: Amplifier. ... 33

(12)

xii

Figure 5. 7: Coil and specimen. ... 34

Figure 5. 8: X-Y table. ... 35

Figure 5. 9: X-Y table software control. ... 35

Figure 5. 10: A steel-based sample from the laboratory. ... 36

Figure 5. 11: A nickel-based specimen with a visible calibrated crack. ... 36

Figure 6. 1: The approach for crack detection limit... 39

Figure 6. 2: The 3-D curve of crack detection limit (from simulated data). ... 40

Figure 6. 3: Detected cracks on the sample – the big one. ... 40

Figure 6. 4: Detected cracks on specimen #01(a) and #51(b). ... 41

Figure 6. 5: Detected cracks on specimen # 57(a) and # 32(b). ... 41

Figure 6. 6 : Crack extraction steps ... 42

Figure 6. 7 : Detected and non-detected cracks ... 43

List of Equations

Equation (2. 1): Temperature at the time and depth z in LT. ... 6

Equation (2. 2): Diffusion length. ... 6

Equation (2. 3): Temperature at the time and depth z in PT... 8

Equation (2. 4): Temperature at the surface in PT. ... 8

Equation (3.1): Voltages ... 11

Equation (3. 2): Voltages in a circuit with two resistors ... 11

Equation (3. 3): Losses power ... 12

Equation (3. 4): Joule heating ... 12

Equation (3. 5): Skin depth ... 14

Equation (4. 1): The governing equation ... 24

Equation (4. 2): The generated resistive heat ... 24

(13)

xiii

List of Abbreviations

ECT Eddy Current Thermography

NDT Non-destructive Testing

IR Infrared Thermography

AC Alternating Current

DC Direct Current

UT Ultrasound Testing

LPT Liquid Penetrant Testing

LT Lock-in Thermography

PT Pulse Thermography

VT Vibro-Thermography

SH Step Heating

TRIR Time-Resolved Infrared Radiometry

IHT Induction Heating Thermography

PDE Partial Differential Equations

IDE Integrated Development Environment

CPU Control Processing Unit

FEM Finite Element Method

(14)

(15)

1

Introduction

Over the last few decades, non-destructive testing (NDT) has been using in many industrial branches, in order to indicate the presence of material discontinuities, such as defects on the surface of material. There are several common methods of NDT, for example: Ultrasound Testing (UT), Liquid Penetrant Testing (LPT), Infrared Thermography (IR) Testing, and so on. In crack inspection, Eddy Current Thermography is the field of IR testing; itis being widely used as a valuable testing method in many industries, particularly in the aerospace industry in which the machine components often have complex structures.

The Computer and Electrical Engineering Department, Université Laval, and the Canada Research Chair in multipolar infrared vision (MIVIM) provide excellent resources for Eddy Current Thermography experiments and simulations, including the electrical devices, a collection of software and powerful computer which are necessary for processing data. In this project, the metallic plate specimens are provided by the industrial partners: L-3 and PWC.

The research work and results are organized in the following chapters.

In chapter 1 of this thesis, the project description is exposed along with the problems which needed to be solved. The information related to the Infrared Thermography part from original documentation of the project CRIAQ-MANU 418 is also included.

Chapter 2 provides the basic information about Infrared Thermography for NDT, the advantages and the applications of IR techniques in industry. Chapter 3 describes general information about Eddy Current Thermography. The theory of ECT and fundamental concepts are reviewed in this chapter.

The detailed information about simulations is provided in chapter 4. This chapter provides the introduction to COMSOL software, and the chosen module: Induction Heating is described in detail. The individual results we obtained during this process are provided as well.

Apparatus and experiments are presented in chapter 5. Detailed information about the needed devices required by experiment is described in this chapter.

Chapter 6 focuses on the research results, including simulation and experiment results. The 3-D curve is proposed in this chapter, and experimental results are matched with that 3-D curve as well.

Chapter 7 gives some remarks, conclusions and future work of this research. Appendix 1 presents the basic steps to simulate ECT in COMSOL software. Appendix 3 gives detailed guide for performing experiments in the laboratory.

(16)

2

Chapter 1 Project description

This research project is part of the project CRIAQ MANU-418: “Automated Non Destructive Testing for the Aerospace Industry”. The information of this chapter is mainly extracted from project description of the project CRIAQ MANU-418 [1].

The main objective of the project CRIAQ MANU-418 is to automate (NDT) systems used in the aerospace industry in order to establish inspection procedures as well as to enhance systems sensitivity, reliability and repeatability. At the moment, these tasks are performed by human inspectors whose diversified experience may lead to variation in results interpretation. A standard robotic system would be used to handle the probe associated with each NDT techniques. Based on data provided by a 3D laser system and using CAD files if available, an initial scanning path will be generated. In case CAD files are not available or not reliable (particularly for in-service or modified components), an initial or largest envelope volume will be used instead. Data fusion algorithms will be used to build a defect database map of the inspected surface and to refine the scanning path in subsequent passes.

Finally, an intelligent expert system will provide the user with a decision on whether a defect is present or not, based on the interpretation of the signals from the probes. The final result of this project will be a functional small-scale robotic NDT inspection workcell that will serve as a benchmark for comparison with human inspectors. In addition, it is proposed to evaluate novel NDT schemes such as Eddy Current-induced Infrared Thermography. This novel scheme allows collecting thermal infrared signatures from induced Eddy currents. Hence, the additional information becomes available from subsurface defects. It is planned to fuse this information with data from the others sensors as well: Fluorescent Penetrant Inspection and Eddy Current Testing.

1.1 Description of the sub-project

The previous paragraph provides introduction to the project CRIAQ MANU-418. In this part, we will describe its sub-project in Infrared Thermography.

As previously mentioned, a standard robotic system will be used to handle the Eddy Current probe to carry the inspection. And a thermal camera (infrared camera) is added to record the thermal signature that appears on the surface of the components following the Eddy current excitation. Finally, the system is fully autonomous and provides a final diagnosis to the human inspectors with a minimum intervention from them.

This approach may bring many benefits to the industry since the position of component referring to the robotic arm is totally relaxed, a conventional Eddy current inspection would be carried out as traditionally done. Moreover, thermographic data is acquired and thus, it is possible to bring additional information to increase the combination of information coming from the different sensing techniques rather than from one technique only.

(17)

3 At the beginning, the 3D camera enables acquiring the part geometry prior to inspection. After the part geometry is calibrated, the robotic arm is enabled in the second step, in order to perform the inspection while maintaining the end effector always perpendicular to the inspected surface and also at the same fixed distance. Moreover, the robot covers the surface to inspect at a constant speed (in a raster fashion). The 3D camera is shut off and only the Eddy Current and Infrared Camera are operated. The Eddy Current and thermal data are acquired at this stage. The defects will be detected automatically by using software.

For automatic detection, it is proposed to analyze independently both channels (Eddy current and IR) and combine the processed data not at the pixel level but rather at a higher level of decision.

1.2 Scientific and technical issues

In order to obtain good results with non-destructive testing system based on Infrared Thermography technique, we have to deal with a number of challenges, including the scientific and technical issues as described below.

The total inspection time should be minimized by optimizing the experiment process. Therefore, it is necessary to use numerical simulations, and COMSOL Multiphysics®

FEM software is the right choice for Infrared Thermography simulation. The detailed information about simulations and COMSOL would be described in chapter 4.

In addition, during the experiments there will be a number of detected cracks and non-detected cracks. Based on the capability of given infrastructure and information about specimen material, we should know the limit of crack detection for cracks in the given metallic specimens. This task would also be extremely challenging.

(18)

4

Chapter 2 Infrared Thermography for Nondestructive

Testing

Infrared Thermography (IR) is an efficient non-destructive testing method. It is being widely used in different fields. It is an inspection method for examination of a part of a specimen, a material, or a complex machine without destroying its usefulness [2].

The basic principle of Infrared Thermography is to thermally excite an object by heating (or cooling) it while using infrared camera to monitor the changes of the object’s surface temperature. Since the temperature flow will be affected by the subsurface discontinuities, and these discontinuities also called defects which could be detected [3]. The knowledge of heat transfer would be presented in the next chapter, when we describe the major NDT method of this thesis: Eddy Current Thermography.

Infrared Thermography can be used in either a passive or an active manner, which are called passive thermography and active thermography, respectively. In the following sections, we will describe the basic information about each approach.

2.1

Passive Thermography

Passive thermography relies on natural heat diffusion on the surface of either a component or a structure, and it is normally employedin production, predictive maintenance, road traffic monitoring, agriculture and biology, medicine, fire forest detection, building thermal efficiency survey, and in NDT.

In passive thermography, the surface temperature for evaluation is measured directly. The different temperature with respect to the surrounding is the most important parameter, often referred to as the ’delta-T’ or the “hot spot.” A delta-T of 1 to 2 Kelvin is generally found suspicious while a 4K value is a strong evidence of abnormal behavior [5]. The features of interest in a given region are naturally at a higher or lower temperature with respect to the surrounding.

2.2

Active Thermography

In contrast to passive thermography, active thermography measures the surface temperature for evaluation after applying a thermal excitation source. There is an external energy source required in this approach in order to produce a thermal contrast between the feature of interest in a given region and its background as shown in Figure 2.1 below:

(19)

5 Figure 2. 1: Experimental setup for active thermography [16].

There is a wide variety of external energy sources available in order to produce a thermal contrast between the subsurface defect and its background. The most common types of these sources can be divided into optical, mechanical and inductive, although many other energy sources can be employed [14].

Depending on the external stimulus, there are a number of different approaches of active thermography which have been developed, such as pulse thermography (PT), lock-in thermography (LT), step heating (SH), vibrothermography (VT) [8].

The sample could be heated from one side and thermal data is collected from the same side, this is the reflection mode. When the observation is from the opposite side, this is called the transmission mode. Reflection mode is used when inspecting defects are close to the heated surface, while transmission is preferred for detection of defects which are closer to the non-heated surface (i.e. deeper defects). The defects can be detected by tracking the anomalous heating distribution in time after application of the thermal excitation.

In the next section, we focus on describing the optical excitation with lock-in and pulse heating modes. Step heating and mechanical excitations with ultrasound are also described.

2.2.1

Lock-in thermography and Optical excitation with LT

The main idea of lock-in thermography is that the temperature modulation induced inside the inspected component propagates as a thermal wave [8, 31, 32].

In optical Lock-in Thermography, absorption of modulated optical radiation results in a temperature modulation that propagates as a thermal wave into the inspected

(20)

6

component. As the thermal wave is reflected at the defect boundary, its superposition to the original thermal wave causes changes in amplitude and phase of the response signal at the surface, which are recorded at the same time using an infrared camera. Sinusoidal waves are commonly used, although other periodic waveforms are possible. Sine waves are more preferable as the frequency and the shape of the response are preserved (i.e. sinusoidal fidelity); only the amplitude and phase of the wave may change. Figure 2.2 shows the schematic configuration of lock-in thermography [6]. Moreover, sinusoidal heating insure single frequency stimulation (i.e. corresponding to the original sinusoidal frequency).

Figure 2. 2 : Schematic configuration of lock-in thermography [6].

The one-dimensional solution of the Fourier’s Law describing temperature T (at the time t and depth z) for a periodic thermal wave propagating through a semi-infinite homogeneous material may be expressed as [9]:

 

z

,

t

T

₀

exp

z

cos(

2 z

t

)

T

_





























Equation (2. 1): Temperature at the time and depth z in LT.

Where T0 is the initial change in temperature produced by the heat source, ω is the

modulation frequency (



2



f , with f being the frequency in Hz), λ is the wavelength; and μ is the diffusion length given by:

f   











2

Equation (2. 2): Diffusion length.

lamp

IR camera

Specimen

(21)

7 Where







/



c

is the diffusivity of material, with



being the thermal conductivity, ρ the density, c the specific heat; and



2



f is the frequency modulation.

The thermal diffusion length



increases with deducing modulation frequency ω as shown in equation 2.2. The probing depth z, for amplitude images is given by the diffusion length, z~μ [10]. For the phase, reported values range from 1.5



to more than 2



[11]. To detect defects on different depths we have to use a range of frequencies roughly corresponding to μ. Deep defects require very low frequency, which of course lengthens the inspection time.

2.2.2

Pulse thermography (PT) and Optical excitation with PT

Pulse thermography (PT) is one of the most common thermal stimulation methods used in active thermography for nondestructive testing. One reason for this is the quickness of the inspection, in which a short thermal stimulation pulse lasting from a few milliseconds for high conductivity materials, such as metal, to a few seconds for low conductivity specimen, such as plastics, is used [5, 12,13].

In optical Pulse Thermography, the surface of specimen is submitted to a short heat pulse using a high power optical source. The duration of the pulse may vary from a few ms (~2-15 ms using flashes) to several seconds (using lamps). Absorption of short time pulse energy elevates the specimen surface temperature. As time elapses and the heating pulse vanishes, the surface temperature will decrease uniformly for a piece without internal flaws.

On the contrary, subsurface discontinuities (e.g. delamination, porosity, inclusions, etc.) will change the diffusion of heat flow and produce abnormal temperature patterns at the surface that can be detected with an IR camera, as shown in figure 2.3 [6].

Figure 2. 3 : Schematic configuration of pulsed thermography [6].

Flash lamp

IR camera

Specimen

(22)

8

The one-dimensional solution of the Fourier’s Law for a Dirac delta pulse propagating through a semi-infinite homogeneous material is given by [33]:

 

_         t z t c Q T t z T







exp 4 , 2 0

Equation (2. 3): Temperature at the time and depth z in PT. Where Q is the energy absorbed by the surface, T0 is the initial temperature.

Considering the surface time evolution, Eq. (2.3) can be rewritten as (z=0):

 

t

e

Q

T

t

T









0

,

0

Equation (2. 4): Temperature at the surface in PT.

Where e



c is the diffusivity, which is a thermal property that measures the material ability to exchange heat with its surrounding.As seen from the previous equation, temperature decreases approximately as t1/2_{(at least at early times).}

2.2.3

Experimental setup for optical thermography

The schematic experimental setup for optical thermography is shown in Figure 2.4.Acquisition was carried out using an FPA infrared camera (Santa Barbara Focalplane SBF125, 3 to 5 μm), with a 320x256 pixel array. Different acquisition frequencies were used in preliminary tests, ranging from 20 to 160 Hz. Two high-power flashes (Balcar FX 60), giving 6.4 kJ each for a ~15ms pulse, were used as heating sources in optical pulsed thermography. And two lamps were used as heating source in optical lock-in and long pulse heating (also called step heating) thermography. The excitation frequency used in lock-in thermography was ranging from 0.1Hz to 0.01Hz. And the pulse duration of step heating is 3~5 seconds in inspections. Data was analyzed with PC using MATLAB software.

(23)

9 Figure 2. 4 : Schematic setup of optical excitation thermography (Reflection mode).

2.2.4

Step heating (SH)

In contrary to Pulse Thermography scheme for which the temperature decays is of interest (after the heat pulse), here the increase of surface temperature is monitored during the application of a step heating (SH) pulse (long pulse). The sample is continuously heated at low power. Variations of surface temperature with time are related to specimen features as in pulse thermography.

This technique of stepped heating is sometimes referred to as time-resolved infrared radiometry (TRIR) [8]. The time resolved means that the temperature is monitored as it evolves during and after the heating process. TRIR finds applications such as for coating thickness evaluation (including multi-layered coatings, ceramics), integrity of the coating – substrate bond determination evaluation of composite structures.

2.2.5

Ultrasound thermography (UT)

Ultrasound thermography (UT) is an active thermography method, and its external energy source is a mechanical excitation. This method was invented in the end of 70’s and has been widely used in 90’s. The basic idea of this method is to induce mechanical waves of high frequencies (usually 15~25 kHz or 40 kHz) into the specimen in order to observe the changes of surface temperature by using an infrared camera.

This method was successfully applied to detect cracks in metals, delaminations in composite materials and other defects both on the surface and subsurface. It is especially used in aerospace and automotive industry.

2.3

Advantage and difficulties of IR thermography

The main advantage of Infrared Thermography in comparison to many other NDT methods is that it makes possible to inspect large areas within a short time and in a safe

Lamp

Lamp IR camera PC

(24)

10

manner without the need to have access to both sides of the component [7]. Moreover, this method has the capacity to provide real time images of any defects which may be present in the inspection area.

For example, with Infrared Thermography we can identify overheating of electrical connections and other machine components. Moreover, scheduling repair is made during planned downtime. This work helps to increase reliability and productivity for the entire operation of products.

Beside the main advantages listed above, IR thermography has more several strengths which make it more useful in some applications where other NDT techniques don’t perform well enough [5, 8, 12, 13, 35]:

 fast and accurate inspection rate;  non-contact approach;

 wide range of applications;

 results are relatively to interpret since these results are obtained in image format and those could be processed by software in order to extract more information;  unique inspection tool for several inspection parts.

However, in addition to the advantages listed above, there are several difficulties of IR thermography as pointed below [5, 8, 12, 13]:

 cost may be a factor for using IR thermography, since the thermo-imaging equipment, data processing and modeling software are expensive;

 effect of thermal loses;

 difficulty in obtaining a uniform thermal stimulation over a large surface;

 IR thermography enables only to inspect a limited thickness of material under the probed surface;

(25)

11

Chapter 3 Eddy Current Thermography

As mentioned in chapter 2, one interesting type of external source in active thermography is inductive excitation which can be employed internally to electro-conductive materials [14].It generates eddy currents at a specific depth which is called penetration depth, or skin-depth. The induced current’s skin depth is determined by the frequency of the excitation. Normally, the range of values of frequencies used in Eddy Current Thermography (ECT) may vary from 20-200 kHz. The temperature distribution is changed if cracks are present in the specimen, since these cracks affect the current flow. And this change can be detected on the surface by an infrared camera. In other words, ECT combines eddy currents and a thermographic NDT technique in order to provide an efficient method for defect detection, such as cracks [4].

Eddy Current Thermography or Induction Heating Thermography (IHT) is the latest development in the field of active thermography, it also received special attention in recent years from researchers around the world [17, 18, 19,20].

In this chapter, the theory and fundamental concepts of ECT are briefly presented. The advantages and limitations of ECT and its applications are also described.

3.1 Fundamental concepts

ECT or Induction Heating occurs due to electromagnetic force fields producing an electrical current in a part of specimen. The part is heated because of the resistance to the flow of this electrical current.

3.1.1 Basic electrical theory

When a voltage is applied to a circuit containing only resistive elements, current flows according to Ohm’s Law:

I = V/R or V = I.R Equation (3.1): Voltages If a circuit consists of more than one element, the overall voltages, resistance and capacitance can be calculated by simple algebra, for example, with two resistors in series, as show in Figure 3.1, current (I) must be the same for both resistors:

V1 =I.R1, V2=I.R2,

Vtotal = V1+V2 = I.R1+ I.R2 = I (R1+R2) = I.Rtotal

Equation (3. 2): Voltages in a circuit with two resistors So Rtotal = R1+ R2.

(26)

12

Figure 3.1 : Resistive elements in circuit.

3.1.2 Resistance and Joule heating

All metals conduct electricity, the resistance of these metals to the flow of electrical current cause losses in power that show up in the form of heat. The losses produced by resistance are based upon the basic electrical formula:

P= i2_R _{Equation (3. 3): Losses power}

Where iis the current value, and R is the resistance.

The resistance appears in two different elements of Eddy Current Thermography, including the induction coil (electromagnetic coil) and the metallic specimen (inspection area).

Joule’s first law, this is also known as the Joule effect, is a physical law that expresses the relationship between the heat generated by the current flowing through a conductor (the metallic material in this project). This phenomenon was studied in the 1840s. It is expressed as the following equation:

Q= I2_Rt _{Equation (3. 4): Joule heating}

Where Q is the heat generated by a constant current I flowing through a conductor of electrical resistance R, for a time t. The unit of Q is joule.

The heating effect of conductors carrying currents is known as Joule heating [28].

3.1.3 Electromagnetic field

Figure 3.2 shows an induction coil with the magnetic fields and induced currents (eddy currents) which are produced by a number of coils.

The induction coil receives alternative electric current from an induction heating control box, which includes two components: amplifier and transformer in our system at the laboratory. This coil becomes the heating source (electrical source), that induces an

(27)

13 equal and opposing electrical current into the metal part of specimen. This current is also called induced current or eddy current.

The alternating current (AC) in an induction coil (heat source) has an invisible force field around it, which is called electromagnetic field. This field also restricts the heat from the heat source to localized areas on the surface immediately adjacent to the coil.

No physical contact is required between the specimen and induction coil, however the induction coil must be placed very close to the specimen as shown in Figure 3.2, the lines of magnetic field concentrate in the air gap between the coil and the specimen.

(28)

14

The rate of heating of specimen is dependent on the frequency and the intensity of the induced current, the magnetic permeability of the material and the resistance of the material to the flow of current [23].

3.1.4 Hysteresis

Hysteresis losses appear in magnetic materials, such as nickel, steel and some other kinds of metals. For example, with the specimens made from carbon steels, when magnetic parts of the specimens are being heated, by induction from room temperature, the alternating magnetic flux field causes the magnetic dipoles of the material to oscillate as the magnetic poles change their polar orientation every cycle. This oscillation is called hysteresis [23]. Moreover, when the dipoles oscillate, the friction produced by this oscillation will generate a minor amount of heat.

3.1.5 Skin depth

In order to make Eddy Current Thermography with Induction Heating an efficient and practical process, certain relationships of the frequency of the electromagnetic field that produce the eddy currents and the properties of the specimen under inspection must be satisfied. These relationships are often referred to as “skin-depth”, or reference depth (depth of penetration).

They are described in the following equation [4, 27]:

Skin depth √ Equation (3. 5): Skin depth

With: angular frequency , permeability µ =

µ

0

µ

r,

resistivity ρ.

The depth of heating depends on the frequency of the magnetic field, the electrical resistivity and the relative magnetic permeability of the specimen.

Figure 3.3 shows reference depths for several materials at different values of temperature. On that figure, we can see that the reference depths decrease with higher frequency and increase with higher temperature.

In other words, the reference depth shows the theoretical minimum depth of heating for which a given frequency will produce at a given power and specimen temperature.

(29)

15 Figure 3. 3 : Reference depth for several materials [22]

Figure 3.4 shows the effect of excitation frequency for ferromagnetic and paramagnetic materials. With paramagnetic materials, the effect of excitation frequency is practically unity, while with ferromagnetic it may be higher.

(30)

16

3.1.5 Heat conduction

The conduction of heat produced by the eddy current is the primary mechanism of heat flow to the interior of a specimen. Losses due to hysteresis are often ignored in the heat content calculations for induction processing because of the minor effect [23].

Mathematical analysis of heat transfer may be difficult because of the interaction of the intense heat produced by the eddy-current heating of the surface. Moreover, the electrical, thermal, and the properties of most materials show a strong dependence on temperature and they vary during the heating process.

3.2 Eddy Current Thermography system

A schematic diagram of the experimental setup of Eddy Current Thermography is shown in Figure 3.5. The main components of ECT system consist of an electromagnetic coil, an infrared camera for capturing infrared images, a specimen under inspection, and a control processing unit.

Figure 3. 5 : A schematic setup of Eddy Current Thermography for NDT [16]. As shown inFigure 3.5, a control processing unit is used in order to control the ET system and process the output data. The infrared images can be analyzed to provide quantitative information of defects inside the inspected specimen.

(31)

17

3.3 Advantages and limitations

Since ECT is an Infrared Thermography Testing method, it has full advantages and difficulties (limitations) from IR thermography that have been described in the previous chapter.

In addition, it has many potential advantages in comparison to heat lamp and sonic excitation. During the excitation process of the coil, the change of temperature is very small, and the material under inspection is not damaged, as heating is limited to a few 0_C

[29].

Besides, the scanning process and necessity of maintaining a close gap between the probed surface and the excitation coil might be seen as a drawback of ECT, depending on the intended application.

3.4 Applications

ECT technique can be used in many industries, in line with other thermographic NDT techniques, such as sonic thermography, particularly in aerospace industry in which engine components often show complex geometries [4, 15, 34].

This method is also used to test the coated components in which cracks may occur under the surface.

(32)

18

Chapter 4 Simulations

Today computer simulation has become an essential part of science and engineering. A computer simulation environment is simply a translation of real world physical-laws into their virtual form. It would be very helpful to know how much simplification takes place in the translation stage, then it helps determining the accuracy of the resulting model. In order to provide efficient solutions for Eddy Current Thermography, it is necessary to use a numerical simulation software package which has multiphysics capability and can be utilized to simulate eddy currents and temperature propagation. Moreover, the numerical software should allow changing the excitation parameters easily [4, 25].

4.1 COMSOL Multiphysic software

It would be ideal to have a simulation environment that included the possibility to add any physical effect to our model. And that is the design goal of COMSOL.

4.1.1 Introduction

COMSOL Multiphysics®_{is an integrated environment, a state of the art software for}

solving systems of time-dependent or stationary second order in space partial differential equations (PDEs) in one, two, and three dimensions, by numerical techniques based on the finite element method (FEM) for the spatial discretization.

COMSOL Multiphysics provides sophisticated and convenient tools for geometric modeling. For many standard problems, it is possible to use provided templates in order to hide much of the complex details of modeling by equations. This is really helpful for the end user.

The step-by-step instruction that is how to model and solve one PDE (in Eddy Current Thermography) will be described in the appendix 1. In this section, the main components of a simple simulation are presented in order to provide general information about modeling in COMSOL Multiphysics.

4.1.2 Working environment

The COMSOL working environment or development environment (DE) is shown in Figure 4.1 this is what we see when we start COMSOL at the first time. It provides a complete and integrated environment for physics modeling and simulation.

(33)

19 Figure 4. 1 : COMSOL integrated development environment.

When we build our model, there are a number of additional windows and widgets that will be added. These windows are described in the following pages.

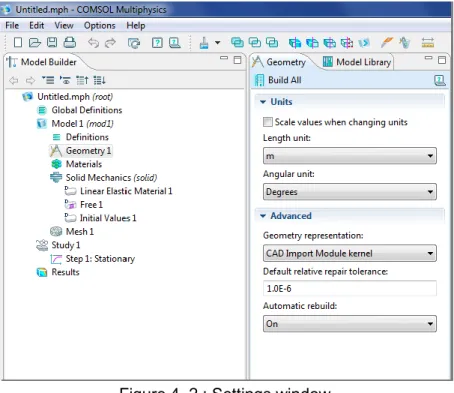
The main window is known as the Settings Window which is shown in Figure 4.2, this window is used for entering all of the specifications of the model, the dimensions of the geometry, the properties of the materials, the boundary conditions and the initial conditions and any other information that the solver will need to calculate the simulation.

Plot Windows

These windows are shown in the blue area in Figure 4.1. These windows are used for the graphical output, and result visualization. There are several Plot windows which can be used to show multiple results simultaneously.

Information Windows

These are the windows for non-graphical information, such as: messages, log information, progress information from solver, and numerical data in table.

(34)

20

Figure 4. 2 : Settings window.

Preferences are settings that affect the modeling environment. This window is shown in Figure 4.3. In this window, we can change settings, such as graphics rendering, number of displayed digits for Results, or maximum number of CPU to be cores used for calculations.

(35)

21

4.1.3 The Model Builder and the Model Tree

The Model Builder is a tool where we can define the model, the analysis of results, and the reports. These works are done by building a Model Tree.

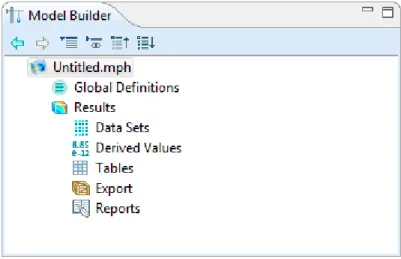
When we start building a tree, a default Model Tree will be added. All of the nodes in the default Model Tree are top-level parent nodes. A Model Tree always consists of a Root node, a Global Definitions node and a Results node as shown in Figure 4.4.

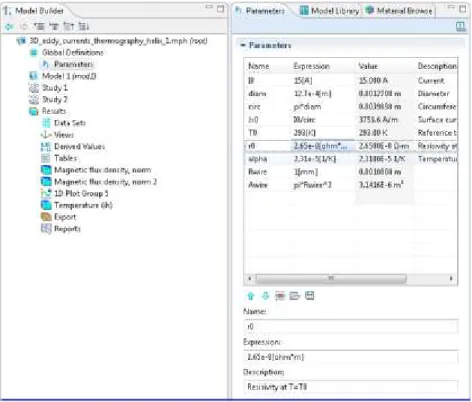
The Global Definitions node is where you define parameters, variables, and functions that can be used throughout the Model Tree. When you create a new definition, for example Parameters definition, a new window will be presented as shown in Figure 4.5.

Figure 4. 4 : Global Definitions and Results nodes.

Parameters are user-defined constant scalar that can be used throughout the Model Tree. A parameter expression may contain numbers, parameters, built-in constants, functions with parameter expression as arguments, and binary operator.

(36)

22

The Result node is where we access the solution after performing a computation and where we find tools for processing the output data. The Result node initially has five sub-nodes as shown in Figure 4.6:

Figure 4. 6 : Result node.

In these five sub-nodes, we can also add additional Plot Group sub-nodes that define graphs to be displayed in the Graphics window or in Plot window. Some of these graphs may be added automatically, depending on the type of simulation we are performing. The Model and Study nodes are usually created by the Model-Wizard when we create a new model. In the Model-Wizard we have to specify the type of physics we are modeling, and the type of Study, such as: time-dependent, frequency-domain, or eigenfrequency analysis.

Figure 4. 7 : Model and Study nodes.

4.1.3 Model library

The Model library is a collection of models with accompanying documentation that include a theoretical background and step-by-step instructions. We can use the Model MPH-files and the step-by-step instructions as shown in Figure 4.8.

(37)

23 Figure 4. 8 : Model Library examples.

4.1.4 Workflow and Sequence of Operations

In the Model Builder window, every step of the modeling process, every step of the modeling process, from defining global variables to the final report of results, are displayed in the Model Tree and many other windows as shown in Figure 4.9

(38)

24

4.2 Mathematical models of Eddy Current Thermography

As described in chapter 3, there is a force field around the induction coil, which is called the electromagnetic field. When this field is applied to a conductive material (the specimen), the temperature of the material would be increased due to resistive heating from the induced eddy current. This temperature is changed according to Joule heating or Joule first’s law.

In simulation, the main goal of mathematical models is to solve the electromagnetic field propagation simultaneously with the heating transfer inside the material. There are a number of essential equations to be solved to describe the electromagnetic field with heat transfer for numerical simulation software packages FEM-based. These equations are given by (4.1) and (4.2) below [15]:

( )

Equation (4. 1): The governing equation

Where ρ is the density, Cp is the specific heat capacity, k is the thermal conductivity, and Q is the inductive heating.

The sum of the generated resistive heat Q is proportional to the square of the magnitude of the electric current density Js. And the electric current density is proportional to the electric field intensity vector E. The following equation expresses these relationships:

| | | |

Equation (4. 2): The generated resistive heat

Where Ϭ is the temperature dependent electrical conductivity of a material Ϭ = Ϭ (T) which is given by the following equation:

( )

Equation (4. 3): The temperature dependent electrical conductivity

Where Ϭ0 represents the conductivity at the reference temperature T0=293Kand α is the temperature coefficient.

The above equation (4.3) describes the dependency of the conductivity on temperature change.

(39)

25 In FEM- based software packages, the essential equations described above are solved by using the time-stepping method. Those packages return accurate results of the heating mechanism around a particular defect [15].

4.3 Simulation results

Through numerical simulation, the underlying phenomena of Eddy Current Thermography on defects in metallic specimens have been investigated.

Induction Heating module in COMSOL Multiphysics®_{is the right choice for ECT}

simulation, because it fully supports simulation in metallic plates. In particular, the temperature dependent thermal conductivity and specific heat capacity are taken into account in the simulation model, and this obviously leads to more precise and real results [4, 30].

Based on the features provided by Inductive Heating module in COMSOL Multiphysics®_,

the capabilities of equipment and the kind of material of specimen in our laboratory, we implemented simulations in both 2-D and 3-D with the parameters values shown in Table 4.1.

Table 4. 1: The thermal and coil’s excitation parameters for simulations

Parameters Values

Current 10A

Number of turns of the coil 10 Radius of wire of the coil 1 mm

Radius of the coil 3 mm Distance between coil and

plate

5 mm

Time of heating 1s

Material of Coil Cooper Material of specimen Nickel

Frequency 30 kHz

In our simulations, we modeled Eddy Current Thermography with the regular main components include air, multi-turns coil, and specimen (including possible flaws). The specimen which contains defects was modeled with dimensions of 25x100x5mm. These dimensions match the real dimensions of given specimens from the industrial partners. The distance between coil and plate mentioned in Table 1 is calculated from the central point of coil’s section to the plate, it is presented in Figure 4.10.

The step-by-step instruction of 3-D simulations is described in Appendix 1. However, the basic steps in every COMSOL Multiphysics® _{simulations are below:}

 First, the Parameters and the Geometry are added. We could use a previously made geometry sequence.

 Then, the materials are chosen for the model, cooper for the coil, nickel for the specimen, and air for the domain surrounding the specimen.

(40)

26

 The physical Induction Heating set-up shows the equations and boundary conditions used to solve the model.

 Finally the mesh is set up and the results are solved.

The results of both 2-D and 3-D simulations are presented in the next sections.

4.3.1 2-D simulation results

Figure 4.10 shows working environment of 2-D simulation in COMSOL Multiphysics®_{4.3a. The parameter values shown in Table 4.1 would be added in}

Parameters part of the Model Tree.

Induction Heating module in COMSOL Multiphysics® _{4.3a provides the possibility to}

simulate the multi-turns coil by adding a simple circle in 2-D. In the setting window of the Multi-Turn Coil property, we have to fill the given parameter values. The reference temperature used in our simulations is always 293K.

In particular, there is an important parameter of the specimen which is the electrical conductivity of a material. As presented in section 4.2, this property depends on the temperature and coefficient resistivity which describes how resistivity varies with temperature.

Figure 4. 10 : 2-D simulation of Eddy Current Thermography.

The result of 2-D simulation is shown in Figure 4.11. We do not see the temperature distribution on the surface of specimen and we do not know how that distribution affects

(41)

27 the cracks if they exist in the specimen, we only see the temperature flow inside the specimen and the environment around. This limits the 2-D simulations.

Figure 4. 11 : Induction heating simulation in 2-D.

4.3.2 3-D simulation result

Figure 4.12 shows working environment of 3-D simulation in COMSOL Multiphysics®_4.3a.

(42)

28

Figure 4. 12 : 3-D simulation of Eddy Current Thermography.

In 3-D simulations, we model a crack with its dimensions as well as the coil with the helix geometry as shown in Figure 4.13. Better visualization is obtained with respect to 2-D simulations.

Figure 4. 13 : Geometry of Induction heating simulations in 3-D.

After one second of heating by performing Study computation node in COMSOL, the specimen is heated, and the distribution of temperature is observed around the crack as

(43)

29 well. The crack area is normally hotter than the surrounding area, because the current density is higher at the crack tip.

Figure 4.14: Induction heating simulations result in 3-D.

Therefore, 3-D simulations are better suited for our application and were essential to establish the results of the next chapter.

The disadvantage of 3-D simulations is that they require much stronger computers with a huge amount of RAM memory. We run our simulations on a computer with 64 Gigabytes of RAM memory.

(44)

30

Chapter 5 Equipment and experimentation

parameters

5.1 Experimental setup

Experiments were done with the typical system setup as shown in Figure 5.1.

Figure 5. 1 : Experiment setup

The main components of the experimental system setup consist of an amplifier, a waveform generator, a transformer for impedance matching, the excitation coil itself, and the infrared camera for capturing infrared images. The excitation of the coil, including the values of current, frequency, voltage, and the different phase between current and voltage are controlled by the waveform generator.

In our experiment, we also use the X-Y table as a robotic arm in order to scan the surface of the specimen.

The experiment diagram is shown in Figure 5.2. The coil excitation values, including the current value and voltage value are checked with the

oscilloscope

.

(45)

31 Figure 5. 2 : Experimental diagram.

In the next sections, general information about all equipment is presented. Moreover, the specimens of interest (metallic plates from P.W.C and a steel-based sample from our laboratory) are also described.

5.2 Infrared Camera

In order to observe the thermal radiation from the surface of the specimen, an infrared camera is used. In our experiments, we mostly use the Jenoptik IR-TCM384 made in Germany by JENOPTIK AG because of its high-performance for stationary NDT applications, it is shown in Figure 5.3 below:

(46)

32

This camera operates in the spectral range (SR) 7.5 to 14 µm. Technical specifications of this kind of camera are presented in Appendix 4. However, there are some features that make it widely used: high frame rate (50/60 Hz), lightweight and compact design, wide measuring range temperature standard (WMRTS).

The Jenoptik IR camera is connected to a personal computer (PC) via a cable according to IEEE 1394. This cable is also called a digital real-time interface. The software VairoCapture is installed on the PC to control the IR camera as shown in Figure 5.4. By using the software VairoCapture, we can change the value of the frame rate before starting a capturing process, the type of output data (IR-Data or RGB-Video).

Since all of output data (the captured images) are stored in RAM memory before we finish capturing, therefore the number of captured images should be taken into account (it should not be over 3000 images) in order to avoid the “out of memory” error for the PC.

Figure 5. 4: IR camera software.

The software VairoCapture supports several output data types, such as: Raw-data images, JPG-images, PNG-images, etc. We can switch the types easily by clicking on “Config” button.

(47)

33

5.3 Amplifier and waveform generator

In order to provide the power for the coil excitation, the amplifier is used. Figure 5.5 shows the amplifier produced by Industrial Test Equipment Co., Inc in our experiments. The meter of the amplifier shows a limited value of the voltage which is 30 Volts.

When the amplifier starts, the power lamp is turned on. This amplifier is well-protected, when its temperature is over the limit, the “overtemp” lamp would be turned on, and then the amplifier would be in the sleep mode.

The amplifier provides the power for transformer as shown in Figure 5.2.

Figure 5. 5:Amplifier.

The above amplifier is controlled by a waveform generator as shown in Figure 5.6. The output signal of waveform generator is connected to the input level of amplifier. The instruction how to control the amplifier by using generator is described in appendix 3. Basically, when the frequency value and the amplitude of generator are changed, then the voltage value of amplifier would be changed accordingly.

With the generator, we normally start with the frequency of 20 kHz, and amplitude of 200mVRMS.

(48)

34

Figure 5. 6:Generator.

5.4Coil

Figure 5.7 shows the coil used in experiments with its properties such as: the number of turns and type of material (copper) which have been modeled in COMSOL simulation section.

Figure 5. 7:Coil and specimen.

5.5 Robotic arm- the scanning table

In our experiments, the X-Y table is shown in Figure 5.8. It supports 3 scanning modes: line scans mode according to two directions: X-axis and Y-axis directions, and raster scan mode. In practice, we normally use the line scan mode in X-axis direction.

(49)

35 Figure 5. 8: X-Y table.

Figure 5. 9: X-Y table software control.

This table is controlled by the software RC/E-Con that is installed on the PC. The detailed instruction is presented in Appendix 2- User guide for the X-Y table.

Normally, the speed is 3 mm/s for scanning the metallic specimens from P.W.C, and 20 mm/s for the sample “– a steel-based sample from our laboratory.

5.6 Specimens

At the beginning of the investigation process, we did experiments on a sample in the laboratory as shown in Figure 5.10.

(50)

36

Figure 5. 10: A steel-based sample from the laboratory.

There are a number of defects with different diameters and depths on that sample. In particular, we tested a number of metallic plate specimens from P.W.C with calibrated cracks as shown in Figure 5.11. The right picture of Figure 5.11 shows a visible crack after it was magnified.

Figure 5. 11: A nickel-based specimen with a visible calibrated crack.

The information about these cracks is known, including the values of length, and depth as shown in Table 5.1 below:

Table 5.1: Crack information for P.W.C specimens.

Specimen # Top/Bottom Length (mm) Length/Width (width~ 0.1mm) Depth (mm) 1 B 0.56 5 0.25 0.63 6 0.29 0.84 8 0.38 9 B 0.89 9 0.4 20 T 0.71 5 0.32 B 0.96 10 0.44 32 B 1.37 15 0.62 2.13 21 0.97

(51)

37 1.57 15 0.71 51 T 0.78 9 0.35 1.17 10 0.53 B 0.68 7 0.31 57 T 1.06 10 0.48 0.63 6 0.29 1.01 10 0.46

(52)

38

Chapter 6 Results

6.1 Crack detection limit

In this section, we would like to propose a new approach based on 3-D simulation results obtained in chapter 4.

Basically, the approach is demonstrated in Figure 6.1. We assume to have two identical specimens: One contains a defect of known size and the other specimen is free of defects.

In the first step, we do the simulations at 5 positions on the specimen which contain a crack as shown on Figure 6.1. We stop at each position about 1 second, and consider the temperature reached from the previous coil position.

Next we get the maximum value of temperature at the central point of defect C(i,j,k), it is called Tmax1.

We then compare Tmax1 with the value of temperature of the corresponding point

C(i,j,k) in the specimen without defect in order to get the difference of maximum

temperature in both cases: with defect and without defect.

Finally, we repeat the above steps with other dimensions of defects in order to generate the 3-D curve shown in Figure 6.2 and discussed below. The dimensions are mainly based on the crack information from P.W.C specimens as discussed in the previous chapter.

(53)

39 Figure 6. 1: The approach for crack detection limit.

To get results as shown in Figure 6.2, we had to perform a large number of 3-D simulations with different values of crack dimensions: about 200 simulations. With a very strong computer with 64 Gigabytes of RAM memory, we could run many simulations rapidly.

On the 3-D curve of Figure 6.2, the vertical axis describes the difference value or contrast of maximum temperatures. Based on the information about the cracks as shown in Table 5.1, we have the width of cracks are the same (~0.1mm). Therefore, the Y axis should describe the ratio Length/Width of defect, and the X axis is the defect depth.

(54)

40

Figure 6. 2: The 3-D curve of crack detection limit (from simulated data).

6.2 Experimental results

After doing the ECT experiment on a steel-based sample from our laboratory, we obtained experimental result as shown in Figure 6.3.There are a number of detected defects on that sample. The purpose of this work is only to show the possibility of detecting defects on a steel-based sample by using ECT testing method.

Figure 6. 3: Detected cracks on the steel-based sample .

In particular, we perform the ECT experiments on nickel-based metallic plate specimens from P.W.C. with the parameters values as shown in Table 4.1; we obtained experimental results (IR images) by using the VairoCapture software control of IR camera. Detected cracks are marked by black circles as shown in the following images.

(55)

41 (a) (b)

Figure 6. 4: Detected cracks on specimen #01(a) and #51(b).

The following figures show cracks of the top side of specimen # 57 and the bottom side of the specimen #32.

(a) (b)

Figure 6. 5: Detected cracks on specimen # 57(a) and # 32(b).

The detected cracks could be extracted and quantified at another stage of this project: the image processing stage. At this stage, the software processes the infrared images; it scans the output folder of VairoCapture software, and then performs the segmentation process. Finally it uses some algorithms in order to extract the crack images. Basically,

(56)

42

these steps are presented in figure 6.6, and were performed by another student working on this global project. These steps are not discussed here [36].

Figure 6. 6 : Crack extraction steps

6.3 Discussion

Based on the known crack information of the specimens from P.W.C. and our experimental results, we could specify the numbers of detected cracks and non-detected cracks. These results are presented in the following table:

Table 6.1 : Statistic information about cracks.

Specimen # Top/Bottom Length (mm) Length/Width (width~ 0.1mm) Depth (mm) Detected (Y/N) 1 B 0.56 5 0.25 Y 0.63 6 0.29 Y 0.84 8 0.38 Y 9 B 0.89 9 0.4 Y 20 T 0.71 5 0.32 Y B 0.96 10 0.44 Y 32 B 1.37 15 0.62 N 2.13 21 0.97 Y 1.57 15 0.71 N 51 T 0.78 9 0.35 Y 1.17 10 0.53 Y B 0.68 7 0.31 Y 57 T 1.06 10 _0.48 Y 0.63 6 0.29 Y 1.01 10 0.46 Y

(57)

43 There are two non-detected cracks in our experiments on given specimens. The reason for this is because the direction of these cracks is not perpendicular to the moving direction of the coil. Therefore, the surface discontinuities are not detected in this case Finally, we match the simulated 3-D curve with experimental results in order to confirm the dimensions for which cracks could be detected or not. The results are shown in Figure 6.7. Detected cracks are marked by black rectangles, and non-detected cracks are specified by red rectangles.

Figure 6. 7 : Detected and non-detected cracks

As seen in Figure 6.7, there is a good matching between simulations and the experiments.

Crack inspection and simulations with Eddy Current Thermography for the aerospace industry