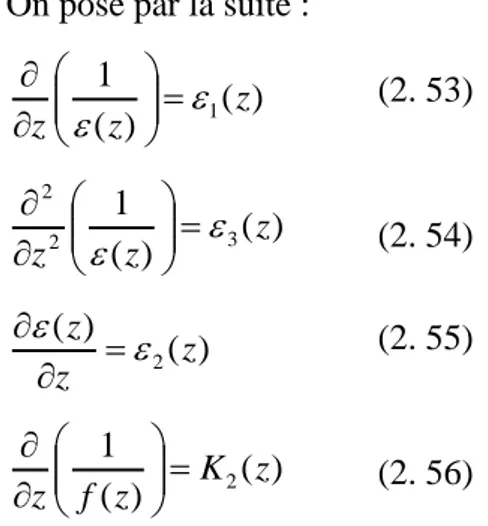Modélisations numérique et théorique du phénomène de la double diffusion dans un milieu poreux à porosité variable. Application extraction de la chaleur en géothermique

UNIVERSITÉ MOHAMMED V

FACULTÉ DES SCIENCES

RABAT

N° d’ordre 2797

THÈSE DE DOCTORAT

Présentée par : Abdellah ELBOUZIDI

Discipline :

Physique

Spécialité :

Mécanique des Fluides et Énergétique

Sur le Thème :

Modélisations théorique et numérique du phénomène de la

double diffusion dans un milieu poreux à porosité variable.

Application à l’extraction de la chaleur en géothermique

Soutenue le 17 octobre 2015, devant le jury composé de:

Président

Gamal ZEGGWAGH : Professeur à la Faculté des Sciences de Rabat. Examinateurs

Mohamed Ouadi BENSALAH : Professeur à la Faculté des Sciences de Rabat. Kamal GUERAOUI : Professeur à la Faculté des Sciences de Rabat.

Ahmed MZERD : Chef du Département de Physique et Professeur à la

Faculté des Sciences de Rabat.

Abderrahim SAMAOUALI : Professeur à la Faculté des Sciences de Rabat. Bennasser BAHRAR : Professeur à l’ENSET de Mohammedia.

1

Dédicace

À

Mes parents,

Ma femme et ma fille,

Mes frères et sœurs,

Tous mes proches,

Tous mes amis,

Tous ceux qui me sont chers,

Tous ceux qui m’ont aidé et

encouragé.

2

Remerciements

Le présent travail a été effectué conjointement au sein du Laboratoire de Thermodynamique et de l’Équipe de Modélisations en Mécanique des Fluides et en Environnement du Laboratoire de Physique Théorique de la Faculté des Sciences de Rabat.

Je suis très sensible à l’honneur que me fait Monsieur Gamal ZEGGWAGH, Professeur de l’Enseignement Supérieur à la Faculté des Sciences de Rabat, en acceptant la présidence du jury, malgré ses multiples occupations et ses nombreuses charges. Qu’il veuille trouver ici, l’expression de ma gratitude pour l’intérêt qu’il a porté à mon travail.

Je tiens à remercier vivement Monsieur Abderrahim SAMAOUALI, Professeur de l’Enseignement Supérieur à la Faculté des Sciences de Rabat, de m’avoir proposé ce sujet. Qu’il trouve ici mes sincères remerciements pour sa disponibilité, ses remarques et ses conseils tout au long de la réalisation de ce modeste travail.

Un très grand merci à Monsieur Kamal GUERAOUI, Professeur de l’Enseignement Supérieur à la Faculté des Sciences de Rabat et Responsable de l’Équipe de Modélisation en Mécanique des Fluides et en Environnement, pour avoir accepté la codirection de cette thèse. Sa disponibilité, son expérience, ses qualités scientifiques, pédagogiques et tout simplement humaines ont été sans conteste à l’origine du si bon déroulement de cette thèse.

Je remercie vivement Monsieur Ahmed MZERD, Chef du Département de Physique et Professeur de l’Enseignement Supérieur à la Faculté de Sciences Rabat, pour l’intérêt qu’il a porté à ce travail et pour avoir accepté de siéger parmi les membres de jury.

Je suis également très reconnaissant envers Monsieur Mohamed Ouadi BENSALAH, Professeur à la Faculté des Sciences de Rabat, pour s’être penché sur mon travail en qualité de rapporteur et pour la pertinence de ses commentaires et remarques.

Je remercie vivement Monsieur Bennasser BAHRAR, Professeur à l’ENSET de Mohammedia, pour l’intérêt qu’il a porté à ce travail, pour avoir accepté d’être rapporteur et d’avoir consacré une partie de son temps à l’analyse de mon travail.

Enfin, je ne saurais oublier mes collègues le Professeur Hassan OUDGHIRI, le Docteur

Mohammed SAMMOUDA, Hamid SAMMRANI et Youssef BELKASSMI. Je suis

3

Résumé

Aujourd’hui, les transferts couplés de chaleur et de masse dans les milieux poreux par convection naturelle et thermosolutale provoquent un vif intérêt dans les domaines industriels et scientifiques. L’avantage pour ces phénomènes de convection naturelle et thermosolutale est dû à leur utilisation dans les divers domaines physiques, technologiques, chimiques et microbiologiques. Parmi les applications potentielles, on peut citer l’extraction de l’énergie géothermique, la croissance cristalline où l'on essaie d'obtenir un monocristal à partir d'un mélange fondu, l’isolation thermique des bâtiments, l’exploitation des réserves pétrolières, la dispersion des polluants dans les aquifères, etc.

Dans la présente étude, on effectue une étude à la fois théorique et numérique du phénomène de la convection double diffusive dans une cavité rectangulaire remplie par un milieu poreux et saturé par un fluide newtonien de propriétés thermo-physiques constantes à l’exception de la densité qui varie linéairement avec la température selon l’approximation de Boussinesq. La paroi latérale de l’enceinte est supposée rigide, imperméable et adiabatique. Les parois horizontales sont maintenues à des températures et concentrations constantes. La porosité du milieu est considérée variable, cette variation est décrite en fonction de la variable verticale de l’enceinte.

L’extension de Darcy-Brinkman a été adoptée pour décrire le mouvement du fluide au sein de la matrice poreuse. Les équations décrivant notre problème physique sont résolues à l’aide de la méthode de Runge-Kutta. Nous avons étudié numériquement l’influence de différents paramètres, entre autres, le nombre de Rayleigh thermique Ra, le nombre de Darcy Da, le nombre de Lewis Le, le nombre de Prandtl Pr, le facteur de rapport de forme, sur le transfert de masse et de chaleur au sein de l’enceinte.

Mots clé : convection naturelle et thermosolutale, milieu poreux, extension de

4

Abstract

Today, coupled transfers of heat and mass in porous medium through natural convection thermosolutal earned a high interest in industrial and scientific fields, the advantage of these natural and thermosolutal convection phenomena is due to their use in the various physical,technological, chemical and microbiological domains. Among the most potential applications, we can cite the extraction of geothermal energy, the crystal growth where one tries to obtain a single crystal from a melt, the thermal insulation of buildings, the exploitation of oil reserves, the dispersion of pollutants in aquifers, etc.

The purpose of this work is to study theoretically and numerically the natural convection and thermosolutal in a square cavity filled with a porous medium saturated by an incompressible Newtonian fluid whose thermo-physical properties of the fluid are considered constant except the density which varies linearly with the temperature and concentration according to the approximation of Boussinesq. The horizontal walls are subjected to constant temperature and concentration. The vertical walls are rigid, adiabatic and impermeable. The porosity is considered variable along the vertical axis of the cavity.

The extension of Darcy-Brinkman was adopted to describe the movement of the fluid within the porous matrix. The equations describing the physical problems are solved by means of the Runge-Kutta method. We numerically studied the influence of various parameters such as the number of thermal Rayleigh Ra, the number of Darcy Da, the number of Lewis Le, the number Prandtl Pr, the aspect ratio factor on the mass transfer and heat within the cavity.

Keywords: natural convection, rectangular cavity, porous media, Rung Kutta,

5

Table des Matières

Liste des sigles et abréviations ……….…...8

Liste des figures………..……….10

Introduction générale ………..………..…….12

Chapitre 1 : Revue bibliographique

………...….…….15

1 .1 Introduction ………..……….….……….…...16

1.2. Historique de la convection thermosolutale en milieu poreux………....17

Chapitre 2 : Modélisation mathématique

………...………...………....26

2.1 Introduction ………..………27

2.2 Hypothèses de travail………..……….….28

2. 3 Expressions de la porosité et la perméabilité ………….……….……..29

2.4 Équations vectorielles ……….……..…..……….…..……...32

2.4.1 Équation de continuité……….……….…....……..33

2.4.2 Équation de conservation de la quantité de mouvement en milieu poreux………...33

2. 4 .3 Équation de l’énergie ……….………...…………36

2.4.4 Transfert de matière dans un milieu poreux………...38

2.4.5 Équation de fonction de courant……….……….….38

2.5 Géométrie et modèle mathématique……….…………..……….…38

2.5.1 Configuration géométrique………..………38

2.5.2 Conditions aux limites……….……40

2.6 Adimensionnalisation………..…………...………...…………43

6

2.6.2 Équation la vorticité……….………..44

2.6.3 Équation de l’énergie………...………..……….45

2.6.4 Équation de matière ……….….………..46

2.6.5 La formulation vorticité-fonction de courant composants de vitesse...…….…….46

2.7 Adimensionnalisation des conditions aux limites………….……….46

2.8 Conclusion……….…………...………..…..47

Chapitre 3 : Résolution numérique

………..……….….48

3.1 Introduction………..……….…49

3.2 Discrétisation des équations………...…..50

3.3 Méthode de résolution………..….….…..50

3.3.1 Équation de continuité ………..……...…….…50

3.3.2 Équation de mouvement………...……….…………...….……51

3.3.3 Équation de l’énergie ………….……….………...…….…..….52

3.3.4 Équation de matière………...………..………..……53

3.3.5 Équation de la fonction de courant………...………...……..……54

3.4 Conditions aux limites………..…..……….56

3.5 Processus de résolution………..………....…..58

3.6 Profil initial………...………...…….58

3.7 Conclusion………...………..…………..……..59

Chapitre 4 : Résultats et Discussions

………...………..………...…….60

4.1 Introduction……….……….……..61

4.2 Cas d’une enceinte carré……….……….……...……62

4.2.3 Effet du nombre de Lewis………..………...62

4.2.4 Effet du nombre de Prandtl……….….……..………67

4.2.5 Effet du nombre de Rayleigh……….……….………...…….…..72

7

4.2.7 Effet du rapport de poussée ……..………..………...……….80

4.3 Cas d’une enceinte rectangulaire………...………..…..………82

4.3.1 Effet du nombre de Darcy ……….………..………….….82

4.3.2 Effet du nombre de Lewis……….……….……….85

4.3.3 Effet du nombre de Prandtl……….………..………..88

4.3.4 Effet du nombre de Rayleigh……… ………...……….…………91

4.3.5 Effet du rapport de forme………..………..……….93

Conclusion générale ………..………..……97

8

Liste des Sigles et Abréviations

C Concentration

D Diffusivité massique

Da Nombre de Darcy 2

/ R K

Dg Diamètre des grains

G Accélération de la pesanteur

H Hauteur de l’enceinte

Imax Nombre maximale des points dans la direction horizontale Jmax Nombre maximale des points dans la direction axiale

K Perméabilité du milieu poreux

ke Diffusivité thermique du milieu poreux _e/

 

C _f

kT Diffusivité thermique du fluide_f /

 

C _f

Le _{Nombre de LewisSc/Pr}

N _{Rapport des poussées}

T S

T

S



C

/





T



Ra

/

LeRa



Nd Nombre des nœuds du domaine d’infiltration

Pv P µs Pression Périmètre Coefficient de frottement Pr _{Nombre de Prandtl} T k /  A Rapport d’aspect H/R

Ra _{Nombre de Rayleigh du fluide}

T T fg TR k  3/ L Longueur de l’enceinte X Coordonnée horizontale Sc As Nombre de Schmidt/D

Surface de la base de cylindre

T Température

T Variable de temps

U Composante horizontale de la vitesse

V Champ des vitesses de darcy

W Composante axiale de la vitesse

Z Coordonnée axiale

ΔT _{Écart de température de référence}

0

T T

T  



ΔC _{Écart de concentration de référence}

0

C C

C  





x

Le pas spatial dans la direction horizontale



z

Le pas spatial dans la direction axiale

9

Indices

0 Référence

axe Sur l’axe du rectangle

C Chaude

F Phase fluide

F Froide

Inf Sur la paroi inférieure

I Indice discret dans la direction horizontale J Indice discret dans la direction axiale paroi Sur la paroi latérale

Sup Sur la paroi supérieure

S Phase solide

∞ Loin des parois

Symboles Grecs



Densité du fluide



Porosité du milieu poreux

 

C Capacité calorifique

 

C m



Capacité calorifique du milieu poreux



Conductivité thermique



 Conductivité thermique du milieu poreux



Rapport des capacités calorifiques

 

C _m/

 

C _f



Viscosité dynamique du fluide



 Coefficient d’expansion thermique



S Coefficient d’expansion solutale



Fonction de la porosité variable



Viscosité cinématique du fluide



Fonction de courant



Composante du vecteur rotationnel des vitesses



Facteur d’homotopie



Facteur de relaxation



Facteur optimal de surrelaxation successive (S.O.R)



Coefficient de pondération

10

Liste des Figures

Figure1 : Récipient cylindrique servant de base au modèle de Janssen……….….29

Figure2 : Dépendance de la porosité en fonction de la profondeur ………..….30

Figure 3 : L’approche prise dans ce cas de transfert thermique……….……...…..36

Figure 4 : La géométrie physique considérée……….……….…………..……..…39

Figure 5 : Représentation du maillage du système physique...…...49

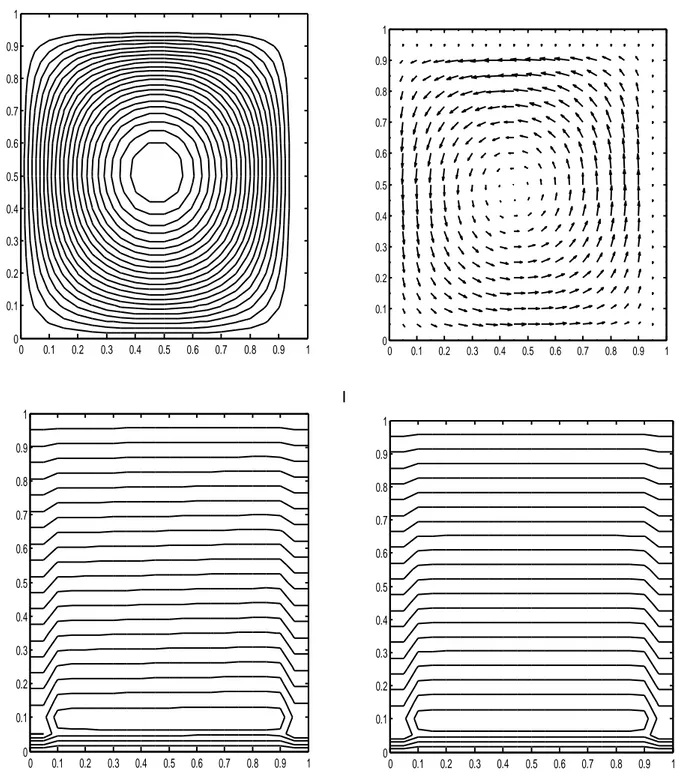
Figure 6 : Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01, Pr=3, A=1, Ra=10000, N=-1 et Le=1….……….…62

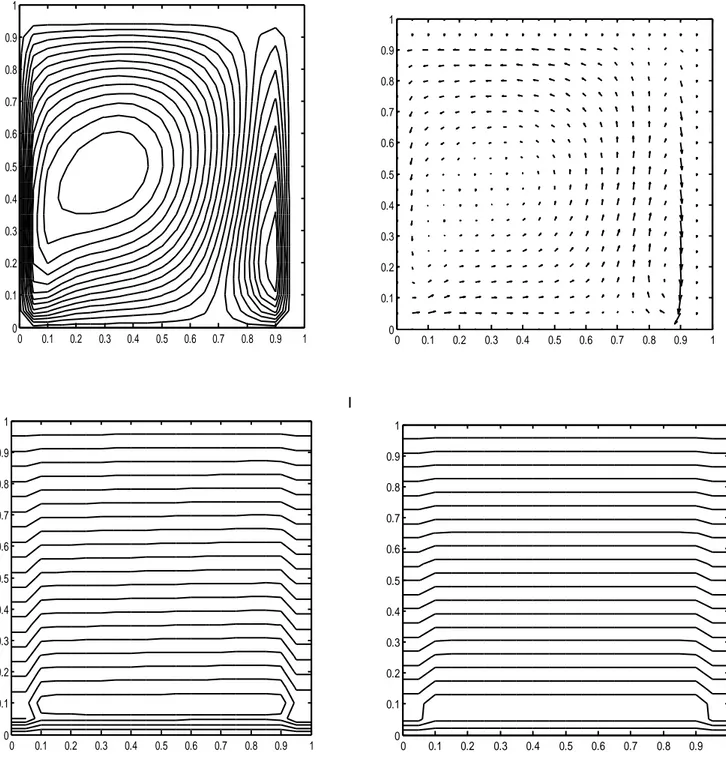
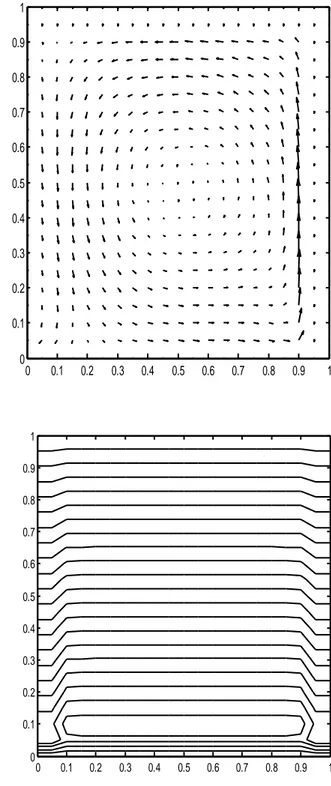
Figure 7: Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01, Pr=3, A=1, Ra=10000, N=-1 et Le=2………...63

Figure 8: Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01, Pr=3, A=1, Ra=10000, N=-1 et Le=3…...…..………..…64

Figure 9: Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01, Pr=3, A=1, Ra=10000, N=-1 et Le=7……….………….65

Figure 10 : Vitesse axiale et vitesse horizontale pour Da=0.01, A=1, Pr=3, Ra=10000, N=-1 et différentes valeurs du nombre de Lewis………...…..………....…...66

Figure 11: Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01, A=1, Ra=10000, N=-1, Le=3 et Pr=3………...…..67

Figure 12: Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01, A=1, Ra=10000, N=-1, Le=3 et Pr=4……….…………...68

Figure 13: Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01, A=1, Ra=10000, N=-1, Le=3 et Pr=5……….………..…69

Figure 14: Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01, A=1, Ra=10000, N=-1, Le=3 et Pr=7………..………...……….….…70

Figure 15 : Vitesse axiale et vitesse horizontale pour Da=0.01, A=1, Le=1, Ra=10000, N=-1 et différentes valeurs du nombre de Prandtl………..……….71

Figure 16: Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01, A=1, N=-1, Le=1 , Pr=3 et Ra=10000…………..………...…….72

Figure 17: Fonction de courant, champ dynamique, isothermes et isoconcentration pour Da=0.01 A=1, N=-1, Le=1, Pr=3 et Ra=106…….………...…..73

Figure 18: Fonction de courant, champ dynamique isothermes et isoconcentration pour Da=0.01, A=1, N=-1, Le=1, Pr=3, et Ra=50.106……….………...….74

11 Figure 19: Fonction de courant, champ dynamique isothermes et isoconcentration pour Da=0.01, A=1, N=-1, Le=1, Pr=3 et Ra=90.106……….……….75 Figure 20: Vitesse axiale et vitesse horizontale pour Da=0.01, A=1, Le=1, Ra=10000, N=-1 et différents valeurs du nombre de Rayleigh.………..…….. ………..………76 Figure 21: Fonction de courant, pour Da=0.01, A=1, N=-1, Le=1, Pr=3, Ra=10000 pour différents valeurs du pas de temps ∆t……….……….…78 Figure 22: Vitesse axiale pour Da=0.01, A=1, Le=1, Ra=10000, N=-1 et différentes valeurs du pas de temps ∆t……….….………78 Figure 23 : Fonction de courant, température et concentration avec Da=0.01, Ra=10000, Pr=3, Le=1, A=1 pour N=1, N=-1, N=-2………..………...………80 Figure 24: Vitesses axiale et horizontale pour Da=0.1, Pr=3, A=1, N=1 et Le=1 pour différentes valeurs de N……….………..………...……….81 Figures 25: Fonction de courant, champ dynamique pour A=10, N=1, Le=1, Pr=3, et Ra=50.103 et Da=0.1, Da=0.01, Da=0.001, Da=0.0001…...……..………..…...…83 Figure 26: Vitesses axiale et horizontale pour Le=1, Ra=50.103, A=10, N=1 et Pr=3 pour différentes valeurs du nombre de Darcy ………...……….……….84 Figure 27: Fonction de courant, champ dynamique pour A=10, N=1, Pr=3 et Ra=50.103, Da=0.1 et Le=0.66, Le=0.83, Le=1, Le=2………...…….……….………..……86 Figure 28: Vitesses axiale et horizontale pour Da=0.1, Ra=50.103, A=10, N=1 et Pr=3 Pour différentes valeurs du nombre de Lewis….…………..……….……87 Figures 29: Fonction de courant, champ dynamique pour A=10, N=1, Ra=50.103, Da=0.1 Le=1 pour Pr=2, Pr=3, Pr=4, Pr=6………….………….………..…………..89 Figure 30: Vitesses axiale et horizontale pour Da=0.1, Ra=50.103, A=10, N=1 et Le=1 Pour différentes valeurs du nombre de parndtl………..………….……….…90 Figure 31: Fonction de courant, champ dynamique pour A=10, N=1, Pr=3, Da=0.1, Le=1 et Ra=5.104, Ra=106, Ra=1.5.106, Ra=2.106………..………..…92 Figure 32: Vitesses axiale et horizontale pour Da=0.1, Pr=3, A=10, N=1 et Le=1 pour différentes valeurs du nombre de Rayleigh ………..…….………..……..…………..93 Figure 33 : Fonction de courant, champ dynamique, Da=0.01, Pr=3, Ra=10000, N=-1 et A=1 pour différents valeurs de A ………..…….………..………....…95 Figure 34 : Vitesses axiale et vitesse horizontale pour Da=0.01, Pr=3, Ra=10000, N=-1 et différentes valeurs de A………..………..………..96

12

Introduction générale

L’étude de la convection naturelle thermosolutale a représenté et représente toujours un champ de recherche très actif à cause de son utilisation dans diverses applications tel que la géophysique, l’océanographique, la croissance cristalline, la convection solaire, la pollution des sols et la géologie, et la géothermie, etc.

Le gradient de température n’est pas le seul champ qui peut créer des mouvements de convection naturelle des particules fluides dus à la différence de la densité mais aussi le champ de gradient de concentration. L’’éxistence d’un champ de gradient thermique et solutale est connu sous le nom de double diffusion (convection thermosolutale). Ce genre de transport convectif en milieux poreux ou fluides intéresse plusieurs industriels et des chercheurs scientifiques de faire plusieurs études sur le phénomène [1-2]. Ce phénomène a été découvert la première fois en 1959 par Stommel [3] dans un contexte océanographique, et sa formulation théorique a été réalisée par Stern [4].

D’une manière générale, la convection peut avoir lieu quand on applique un champ de gradient thermique sur un fluide. Cela entraîne la création d’une différence de masse volumique qui engendre, dans certains cas, des mouvements naturels de la matière. Cette dernière a tendance à monter grâce à la Poussée d’Archimède lorsqu'elle est chaude (donc moins dense) et à redescendre une fois refroidie créant ainsi des mouvements circulaires pour assurer les échanges thermiques entre les milieux chauds et les milieux froids. Ce phénomène assure les échanges de chaleur dans la plupart du temps dans notre environnement quotidien. En effet, l'eau dans une casserole, l’équilibre thermique entre l’air de notre maison et l’extérieur se font par convection naturelle. Plus encore, la pollution due aux gaz émis par les automobiles et les usines industrielles doit être évacuée assez rapidement par les mouvements atmosphériques, sinon l'air deviendrait irrespirable. C’est à cause que la température est plus élevée au sol qu'en altitude que des mouvements de convection assurent cette évacuation.

La résolution d’un problème de type convection naturelle (thermique ou thermosolutale) au sein d’un milieu poreux revient à déterminer les champs de température, de concentration et de vitesse ainsi que l’intensité de l’écoulement en fonction de divers paramètres du problème [5-6].

L’originalité de notre travail consiste à traiter théoriquement puis numériquement la convection thermosolutale en milieu poreux. Notre objectif est d'aboutir à une modélisation

13 complète des écoulements et des transferts thermiques et solutaux couplés dans le cas d’une cavité de géométrie rectangulaire remplie d'un milieu poreux homogène et saturé par un fluide newtonien. Toutes les études précédentes portaient sur des cas où on applique des flux de masse et de chaleur constants dans la même direction. Cependant, dans notre étude nous traiterons le cas de flux croisés sur les parois de la cavité avec différentes conditions aux limites et nous nous intéresserons aux effets ainsi engendrés sur l’écoulement interne et sur les transferts de chaleur et de masse dans le système. Les approximations de Darcy et de Boussinesq [7] seront adoptées pour décrire l’écoulement doublement diffusif dans la cavité. Toutes les études précédentes considéraient la porosité uniforme à l’exception du travail de Monsieur Sammouda [8] qui a considéré la porosité variable mais suivant l’axe perpendiculaire à l’axe du cylindre. Dans cette étude, nous traiterons le phénomène avec porosité variable suivant l’axe verticale.

Nous considérons que les propriétés thermodynamiques sont constantes excepte la densité qui varie linéairement avec la température et la concentration selon l’approximation de Boussinesq. Des conditions aux frontières de type Dirichlet (température et concentration constantes) ont été imposées sur les parois supérieure et inférieure de l’enceinte. La paroi latérale est rigide, imperméable et adiabatique.

À cette fin, ce mémoire de thèse est structuré de la façon suivante :

dans le premier chapitre, un travail de recherche bibliographique portant sur la convection thermosolutale dans les milieux poreux sera présenté, en essayant de rappeler certains travaux de recherche effectués dans ce domaine de recherche, il sera suivi dans le second chapitre par la formulation mathématique du problème où les équations de bases décrivant le système et les conditions aux frontières associées seront présentées, le troisième chapitre présente la méthode de résolution numérique des équations aux dérivées partielles qui sont formulées sous la forme vorticité-fonction de courant (formulation plus commode dans les écoulements bidimensionnels). À cette fin, la méthode de Runge-Kutta sera utilisée pour discrétiser les équations de conservation. Quant à la fonction de courant, elle sera résolue par la méthode S.O.R (Simultaneous Over-Relaxation), le quatrième chapitre porte sur les différents résultats obtenus dans cette thèse et leurs discussions.

14 Ce dernier chapitre sera divisé en deux parties. La première partie est consacrée à la discussion des résultats obtenus pour le cas d’une cavité carrée. La deuxième partie portera sur une cavité rectangulaire.

Ce document est terminé par une conclusion générale qui retraçe les principaux résultats trouvés le long de cette étude ainsi que les perspectives à envisager dans le futur et qui peuvent faire l’objet de travaux complémentaires.

15

Chapitre 1 :

16

1 .1 Introduction

Durant les dernières décennies, le phénomène de la convection naturelle a été largement abordé. Il s’agit d’un mode de transfert de chaleur d’un milieu chaud vers un milieu froid sous l’action d’un mouvement des particules de fluides produite par des effets de Poussée d’Archimède quand on applique un champ de gradient de température. Dans le cas le plus fréquent, les deux paramètres responsables de ces mouvements convectifs sont les gradients thermiques et de concentration. Ils peuvent agir ensemble ou bien en opposition. Ce phénomène cruciale est connu sous le nom de convection thermosolutale ou double diffusion. Le phénomène de la convection peut se produire dans les liquides, tels que les océans, ou dans les milieux poreux, tels que dans les systèmes géothermiques. Rappelons que la porosité est reliée au vide (appelé pores) qui se trouve dans une matrice solide constitué par des grains consolidés. Une synthèse des travaux antérieurs est présentée dans le livre de Nield et Bejan [5] pour les milieux poreux et dans le livre de Brandt et Fernando [9] pour les milieux fluides. Le but de ce chapitre est de présenter les travaux de recherche déjà menés sur le

phénomène de la convection naturelle thermosolutale dans les milieux poreux afin de justifier le choix de travail.

1.2 Historique de la convection thermosolutale en milieu poreux

Pour étudier le phénomène de la convection dans un milieu poreux, il faut connaître le mouvement du fluide au sein de cette matrice poreuse. Mais il est difficile de connaitre précisément le mouvement de fluide dans le milieu poreux de façon exacte. D’où les chercheurs essaient de donner un modèle pour décrire d’une façon macroscopique le mouvement des particules fluides au sein d’une couche poreuse ainsi que le transfert de chaleur et de matière engendré.

La convection thermosolutale (l’existence d’un gradient thermique et solutale) est

considéré par les industriels et les scientifiques comme un domaine très important et très vif à cause de la multitude d’applications telles que les systèmes d’énergie géothermique, l’exploitation des réserves pétrolières, la dynamique du noyau terrestre, la croissance cristalline où l'on essaie d'obtenir un monocristal à partir d'un mélange fondu, siège d'une solidification par ségrégation, la pollution des sols et la géologie. Cela a motivé les chercheurs et industriels à mener des recherches dans ce cadre dont l’objectif principal est de comprendre les différents mécanismes résultants des mouvements convectifs engendrés.

17 H. Darcy [10] [11] donne un modèle empirique simple pour décrire le mouvement de fluide au sein d’une couche poreuse. Ce modèle est limité à des écoulements lents. Plus tard, ce modèle a été corrigé pour être mieux adapté à des écoulements à grand nombre de Reynolds. En se basant sur des données expérimentales, un terme non-linéaire de second ordre entre la vitesse d’infiltration et le gradient de pression a été ajouté par Forchheimer [12] pour tenir compte des effets d’inertie pour des écoulements à grandes vitesses. Les effets des parois (contraintes visqueuses) sont pris en considération en modifiant la loi de Darcy, la modification a été présentée par Brinkman [13] [14].

D. Nield [15] est le premier qui a réalisé une étude sur le phénomène de convection thermosolutale dans un milieu poreux isotrope horizontal d’extension infinie chauffé par le bas et soumis à un gradient de concentration vertical. Cette étude a permis de déterminer le nombre de Rayleigh critique et aussi l’auteur traite ce phénomène de la convection pour différentes conditions aux frontières. Il a montré que des écoulements convectifs oscillants peuvent se déclencher à des Rayleigh inférieurs au nombre de Rayleigh supercritique lorsque le soluté joue un rôle stabilisant et la chaleur celui d’un déstabilisant.

Ce travail a été réétudié d’une manière plus complète par Taunton et al [16]. Ces auteurs ont distingué entre trois régimes : un premier régime stable correspondant à l’état de repos du fluide, un second régime dit oscillant caractérisant la transition entre le régime stable et le régime oscillant et un dernier régime caractérisant l’apparition du phénomène convectif pour des nombres de Rayleigh supérieurs au nombre de Rayleigh supercritique.

L’étude du phénomène de la convection double-diffusive dans une couche poreuse horizontale en utilisant la loi de Darcy étendue par Brinkman (des effets des contraintes visqueuse sont pris en considération) a été effectuée par Poulikakos [17] pour caractériser le mouvement de fluide au sein de cette couche.

Tyvand [18] a étudié théoriquement le début de la convection dans une couche poreuse horizontale homogène et anisotrope. L’auteur a supposé que la diffusivité thermique et la diffusivité solutale sont constantes dans la direction horizontale.

Trevisan et Bejan [19] ont étudié théoriquement et numériquement le phénomène de la convection thermosolutale dans une couche poreuse isotrope chauffée et salée par le bas pour des grands nombres de Rayleigh thermiques.

Murray et Chen [20] ont été les premiers à étudier expérimentalement la convection double diffusive dans un milieu poreux. Leur dispositif, constitué d’une boîte métallique

18 remplie de billes de verre saturées avec de l'eau distillée, était soumis à des flux de masse et de chaleur.

Fournier [21] a appliqué le modèle de la convection double diffusive dans l’étude des roches hétérogènes des systèmes géothermiques réels. Ce modèle tient compte des gradients solutaux verticaux et latéraux. Il a proposé pour les futures études, de tenir compte d’une part, de la décroissance de la salinité et la température du bas vers le haut et du centre vers les côtés du système, et d’autre part, d’un transfert de chaleur très élevé au-dessus du système accompagné d’une densité relativement uniforme du fluide.

Rosenberg et Spera [22] ont effectué une étude du phénomène de transfert de masse et de chaleur au sein d’une cavité remplie par une matrice poreuse soumise à une gradient de température verticale et une variété de conditions initiales et des conditions aux frontières. Ce travail montre que la structure et la dynamique de l’écoulement ainsi que le transfert de masse et de chaleur dépendent fortement du rapport des poussées des forces solutale et thermique pour des nombres de Rayleigh et Lewis constants.

Une étude de la convection thermosolutale au sein d’un milieu poreux isotrope obéissant à des flux uniformes de chaleur et de soluté imposés à la paroi inférieure a été réalisée par Mamou et al [23], et Amahmid et al [24]. Une bonne concordance a été trouvée dans cette investigation entre les résultats obtenus analytiquement par Sen et al [25] et numériquement par Alavyoon [26]. Ils se sont focalisés particulièrement au cas où les forces de poussée thermiques et solutales s’opposent et sont de même intensité. Le nombre de Rayleigh critique marquant l’amorcement du phénomène de la convection a été calculé analytiquement pour différents nombres de Lewis et Darcy. Ces auteurs ont trouvé que le nombre de Rayleigh thermique critique augmente lorsque le nombre de Darcy augmente pour un nombre de Lewis égal à 1. Pour des nombres de Rayleigh supérieurs au nombre critique l’augmentation du nombre de Darcy réduit l’intensité de l’écoulement ainsi que le taux de transfert thermique et solutale.

Karimi-Fard et al [27] ont étudié numériquement, en utilisant la méthode des volumes finis, l’effet des termes de Forchheimer et de Brinkman sur l’écoulement convectif dans une cavité poreuse carrée.

Amahmid et al [28] et Mamou et al [29] ont utilisé le modèle de Brinkman pour étudier analytiquement et numériquement la convection naturelle thermosolutale induite dans une couche poreuse verticale soumise à des flux de chaleur et de masse uniformes. Ils se sont

19 intéressés particulièrement au cas où les forces de volume thermiques et solutales sont opposées et de même intensité. Les nombres de Rayleigh critiques caractérisant l’apparition des mouvements convectifs sont calculés analytiquement en fonction des nombres de Lewis et de Darcy. Il a été trouvé que le nombre de Rayleigh thermique critique augmente lorsque le nombre de Darcy augmente ou lorsque le nombre de Lewis tend vers l’unité. De plus, il a été montré que l’augmentation du nombre de Darcy induit une diminution de l’intensité de l’écoulement et des transferts thermiques et massiques. Par contre, l’augmentation du nombre de Rayleigh cause l’augmentation monotone de l’intensité de l’écoulement. Les résultats du milieu fluide ont été également obtenus à partir de la présente solution pour des nombres de Darcy suffisamment élevés.

Dans une étude appuyée sur la stabilité linéaire, Mahidjiba et al [30] illustrent l’effet des conditions aux limites thermiques et solutales de type Neumann et Dirichlet respectivement, sur la convection thermosolutale dans une cavité rectangulaire horizontale remplie par un milieu poreux isotrope à porosité uniforme. Les auteurs montrent alors qu’il existe trois nombres de Rayleigh critiques, le nombre de Rayleigh supercritique, le nombre Rayleigh sur-critique et le nombre Rayleigh oscillant. Ils montrent aussi que pour des conditions aux limites thermique et solutale de type Dirichlet et Neumann respectivement, la structure de l’écoulement convectif est monocellulaire indépendamment de la valeur du rapport de forme pour (N×Le < -1). Alors que pour un rapport de forme pour (N×Le ≤ -1), l’écoulement est inconditionnellement stable selon la stabilité linéaire.

Une étude analytique et numérique concernant le transfert combiné de chaleur et de masse dans une cavité rectangulaire remplie par un milieu poreux homogène et présentant une anisotropie thermique a été effectuée par R. Bennacer et al [31]. Le modèle adopté est de Darcy-Brinkman pour caractériser l’écoulement du fluide dans le milieu poreux. Une situation où le transfert de masse est maximal a été établie pour une valeur critique du taux d’anisotropie thermique. Les auteurs ont établi une relation globale permettant de prédire le transfert de masse pour les milieux thermiquement anisotropes en régime de Darcy. Un critère de validité de cette corrélation a également été défini.

Bourich et al. [32] ont analysé numériquement la convection double diffusive dans une cavité poreuse carrée. Les parois horizontales sont maintenues à des températures constantes alors que les parois verticales sont alimentées par des concentrations différentes.

20 Nithiarasu et al [33] ont étudié la convection naturelle dans une cavité rectangulaire remplie par un milieu poreux non-Darcien en tenant compte des effets des contraintes visqueuses et d’inertie dans l’équation de mouvement qui est réduite aux équations de Navier-Stokes. La porosité est supposée variable selon une loi empirique qui suit une fonction exponentielle. L’investigation est faite pour différentes valeurs de nombres de Darcy et de Rayleigh.

Mrabti [34] a étudie le phénomène de la convection naturelle dans une cavité cylindrique de rapport d’aspect égal à l’unité, un milieu poreux saturé par un fluide newtonien de nombre de Prandtl égal à 0.71. L’enceinte est chauffée par le bas, la paroi latérale est supposée rigide, imperméable et adiabatique. L’auteur a observé qu’en augmentant le nombre de Rayleigh thermique la structure de l’écoulement devient bicellulaire avec une intensification de l’écoulement lorsqu’on augmente la porosité du milieu. Cette structure bicellulaire disparait lorsque le nombre de Darcy augmente.

Le modèle de Darcy avec l'approximation de Boussinesq a été employé pour étudier la convection naturelle double diffusive dans une cavité peu profonde poreuse par Kalla et al. [35]Les parois horizontales sont soumises à des flux uniformes de chaleur et de masse, tandis que les parois verticales sont exposées a un flux de chaleur. La méthode des différences finies a été employée pour obtenir la solution numérique des équations gouvernantes. Les équations de l'énergie et de concentration sont résolues avec la méthode A.D.I (Alterning Direction Implicit). Le champ de la fonction de courant est obtenu avec la méthode S.O.R (Successive Over Relaxation). Un bon accord est entre une solution approximative analytique et les simulations numériques. Les observé résultats analytiques indiquent que pour la convection supercritique où les deux contributions solutale et thermique se déstabilisent, il y a trois solutions différentes. Une de ces solutions est instable pour une gamme de données des paramètres gouvernants, à condition que le nombre de Rayleigh thermique RaT soit plus grand

que la valeur critique qui dépend du nombre de Rayleigh solutale Ras et de Lewis. D'autre

part, pour la convection sous critique, qui se produit quand les deux forces du nombre buoyancy sont opposées, il y a cinq solutions différentes (dont deux sont instables). L'existence des solutions multiples quand RaT = 0 a aussi été démontrée.

Les recherches menées dans le phénomène du transfert conjugué de chaleur et de masse dans les milieux poreux saturés par un fluide non-Newtonien est très important, cela est due à leurs diverses applications industrielles. Ching-Yang Cheng [36] a étudié le phénomène du

21 transfert de masse et de chaleur par convection naturelle d’une plaque maintenue à des flux de chaleur et de masse variables dans un milieu poreux saturé par un fluide non-Newtonien suivant une loi de puissance. L’auteur a observé que l’existence d’un gradient de pression dans la loi de puissance du fluide réduit le profil de la vitesse ainsi que le transfert de chaleur et de masse traduit par les nombres de Nusselt et Sherwood respectivement. Une augmentation de la composante de la loi de puissance améliore le transfert thermique et solutale.

La convection naturelle double diffusive dans une cavité horizontale remplie par un milieu poreux saturé a été examinée numériquement par Mohamad et al. [37]. Le modèle de Darcy- Brinkman a été adopté dans l'analyse. La cavité est chauffée et refroidie le long des parois verticales et le gradient solutal est imposé verticalement. La méthode des volumes finis a été employée pour la discrétisation des équations du système et l’algorithme SIMPLER pour le couplage pression vitesse. Les résultats ont été obtenus pour un rapport d'aspect de deux, le nombre de Prandtl était de 0.71 (air) et le nombre de Lewis était de 10 (le carburant d'hydrocarbure). L’écoulement devient instable pour une gamme finie du rapport de buoyancy thermique et solutal et il est possible d'obtenir des solutions différentes dans cette région. Le fluide fortement stratifié peut supprimer la convection thermique et le transfert de chaleur devient conductif.

La convection naturelle double diffusive dans une cavité anisotrope poreuse a été examinée par Bera et al. [38] Le modèle de Darcy a été utilisé pour décrire le problème. Les effets des paramètres anisotropes sur l'existence d'oscillations instables permanentes et des solutions multiples stationnaires ont été étudiés. L’étude de solutions analytiques a été considérée comme une vérification des résultats numériques. La direction locale d’écoulement change a cause de la variation des couches thermique et de concentration et des paramètres anisotropes. Il a été observé qu'une petite rotation du tenseur de perméabilité apporte un changement significatif au niveau de la force d’écoulement et au niveau des profils de température et de concentration. En général, la chaleur et la masse suivent le modèle complexe selon l'interaction entre les coefficients de diffusion et le rapport de buoyancy.

Khanafer et al [39] ont étudié numériquement la convection mixte avec un transport de chaleur et de masse dans une cavité rectangulaire avec couvert mouvant remplie d’une matière poreuse saturée avec un fluide non-Darcien. Les deux parois horizontales sont soumises à différentes températures et concentrations, tandis que les deux parois verticales sont imperméables et fixes. La méthode des volumes finis a été utilisée avec la procédure de

22 résolution A.D.I pour traiter l’équation de transport. Les résultats ont montré que le mécanisme de transfert de chaleur et les caractéristiques de flux à l'intérieur de la cavité dépendent fortement du nombre de Richardson. Ces résultats indiquent aussi que le rapport de buoyancy, le nombre de Darcy, le nombre de Lewis et le nombre de Richardson ont un grand effet sur le phénomène de double diffusion.

La convection naturelle double diffusive dans une cavité mince verticale poreuse est étudiée, analytiquement et numériquement par Bahloul et al [40].Les forces de buoyancy qui provoque le mouvement de fluide résultent de l'imposition d’un gradient vertical de température et d’un gradient horizontal solutale. La solution analytique a été obtenue pour un fluide stratifié dans une cavité avec un rapport d’aspect élevé et validé par l’étude numérique. En absence d'un gradient horizontal solutale (N = 0), la solution prend la forme de la bifurcation de Bénard [1]. L'asymétrie résulte de l'imposition d'un petit rapport de buoyancy (N << 1). La solution numérique des équations gouvernantes indiquent que pour le rapport de forme de la cavité A<< 1, le flux est parallèle dans la partie centrale de la cavité tandis que les champs de température et de concentration sont linéairement stratifiés. L'existence de solutions multiples, pour une gamme donnée des paramètres gouvernants a été démontrée analytiquement et numériquement pour le cas des petites valeurs du rapport de buoyancy. Ainsi selon les conditions initiales « des flux naturels » et « des flux antinaturels » peuvent être observés dans le système.

Fu-Yun Zhao et al [41] ont étudié la convection double diffusive dans une cavité rectangulaire d’une extension infinie. La cavité est partiellement chauffée et salée par une des parois verticales, alors que le reste est supposé rigide imperméable et adiabatique. Une série d’essais numériques a été menée pour différentes valeurs des nombres adimensionnels de contrôle, à noter, le nombre de Darcy, le nombre de Lewis, rapport des poussées et la localisation du segment qui représente la source de chaleur et le soluté. Il a été remarqué que la localisation du segment source de chaleur et de concentration a une influence sur la structure d’écoulement ainsi que sur le taux de transfert de chaleur et de masse. L’augmentation du nombre de Lewis améliore considérablement le taux de transfert de masse et une nette diminution du taux de transfert de chaleur.

Chamkha et Hameed [42] ont fait une généralisation des travaux réalisés par Nishimura [43] pour inclure l'inclinaison de la cavité, et ceux de Mamou et al [44] pour tenir compte du cas où les forces de volume sont différentes de l’unité. Ils ont constaté d’une part, que les

23 mécanismes de transfert de chaleur et de masse et les caractéristiques de l'écoulement sont fortement dépendants de 1/Da et de l'angle d’inclination. D’une autre part, les nombres moyens de Nusselt et de Sherwood sont minimums pour n'importe quelle valeur de 1/Da et pour N ≈1,2. Ils ont aussi démontré que l’augmentation de l’angle d’inclinaison de la cavité diminue le nombre moyen de Nu et Sh quand les forces de volume sont dominées par les effets thermiques.

Marcoux et al [45] ont étudié les régimes d’écoulement dans une cavité verticale soumise à des flux de chaleur et de masse. Karimi-Fard et al [46] ont considéré des conditions aux frontières de type Dirichlet (température et concentration constantes sur les parois verticales de la cavité poreuse) et Mojtabi et Charier [47] ont étudié le cas d’une cavité inclinée soumise à des conditions aux frontières de type Neumann.

L’effet des parois n’a pas d’influence sur l’écoulement de fluide d’une manière directe (effet des contraintes visqueuses). Mais elles peuvent avoir une influence sur l’arrangement des grains constituant la matrice poreuse créant ainsi une désorganisation qui se traduit par une augmentation de la porosité au voisinage des parois. Une relation empirique traduisant cette variation de la porosité près des parois est présentée dans les travaux de ces auteurs [48-54].

Shih-Wen Hsiao et al [55] ont étudié numériquement la convection naturelle d’une cavité cylindrique chauffée et incorporée dans un milieu poreux. La porosité varie approximativement suivant une fonction exponentielle au voisinage de la paroi latérale du cylindre. Les effets non-Darciens et la dispersion thermique sont pris en considération dans l’équation de mouvement et l’équation d’énergie. Comme résultats, ils ont trouvé que la variation de la porosité tend à augmenter le gradient de la température près de la paroi latérale de la cavité. L’effet de la dispersion thermique est négligeable pour des nombres de Rayleigh petits. En tenant compte de la variation de la porosité et de la dispersion thermique, les nombres de Nusselt moyens qui traduisent le taux de transfert thermique sont proches de ceux trouvés expérimentalement.

Des résultats qualitativement semblables à ceux trouvés par Shih-Wen Hsiao et al sont obtenus par Jiin-Yuh Jang et al [56], D. Pal et I.S. Shivakumara [57], A.M. Elaiw [58] qui ont étudié l’effet de la variation de la porosité sur la convection naturelle d’une plaque semi-infinie incorporée dans un milieu poreux.

24 N. Retiel et H. Bougurra [59] ont étudié l’influence du nombre de Rayleigh thermique et du nombre de Lewis sur la structure de l’écoulement et sur la distribution de la température et de concentration du phénomène de convection thermosolutale dans une cavité demi-cylindrique horizontale fermée, chauffée et salée par la paroi horizontale qui coupe le cylindre verticalement en deux. L’investigation est faite pour différents rapports des poussées des forces themique et solutale N dans le cas où les forces de poussé s’opposent (N<0) ou s’additionnent (N>0), pour un nombre de Prandtl=0,7. D’après les résultats trouvés, les auteurs ont remarqué que les profils de température et de concentration varient considérablement en fonction des nombres de Rayleigh thermique et du nombre de Lewis.

Récemment, A.C. Baytas et al [60] ont analysé numériquement la convection double diffusive dans une cavité rectangulaire remplie partiellement par un milieu poreux dans le coté inférieur de la cavité et saturé par un fluide newtonien. Alors que la partie supérieure de la cavité est remplie par un fluide newtonien. Les parois horizontales sont maintenues à des températures et concentrations uniformes. Les parois horizontales sont supposées rigides imperméables et adiabatiques. Pour décrire le mouvement du fluide dans la matrice poreuse, on adopte l’extension de Brinkman-Forchheimer de la loi de Darcy. Pour passer du milieu fluide au milieu poreux on considère les conditions de continuité pour la température, la concentration et la vitesse. Les auteurs montre que lorsque le facteur de forme A augmente la structure présente un écoulement multicellulaire avec un changement de sens pour quelques cellules. Le taux de transfert thermique et solutal (le nombre de Nusselt et et le nombre Sherwood respectivement) s’améliore sur la paroi active de la cavité avec l’augmentation du facteur de forme A.

Très récemment, des études théorique et numérique du phénomène de la convection double diffusive ont été effectuées par Sammouda [8]. L’auteur a considéré une cavité cylindrique remplie par un milieu poreux et saturé par un fluide newtonien, les propriétés thermo physiques sont constantes, à l’exception de la densité qui varie linéairement avec la température selon l’approximation de Boussinesq. La paroi latérale de l’enceinte est supposée rigide, imperméable et adiabatique. Les parois horizontales sont maintenues à des températures et concentrations constantes. La porosité du milieu est considérée variable, cette variation est décrite par une loi empirique exponentielle en fonction du rayon de l’enceinte. L’effet des nombres sans dimension, de Rayleigh thermique (Ra), de Darcy (Da), de Prandtl

25 (Pr), de Lewis (Le) et le rapport de poussée (N), sur l’écoulement et les transferts de masse et de chaleur a été analysé.

26

Chapitre 2 :

27

2.1 Introduction

Pour atteindre les objectifs visés, il est nécessaire de définir une méthodologie bien appropriée afin d’établir un code numérique valide qui permet de simuler tous les phénomènes mis en jeu. Nous présentons dans cette partie la formulation mathématique générale du problème.

La notion de modèle a été introduite pour décrire le mouvement du fluide et le transfert de chaleur et de matière au sein d’un milieu poreux de façon macroscopique pour faciliter la description du mouvement d’un fluide dans une matrice poreuse.

Le modèle de base le plus simple qui permet de décrire le mouvement d’un fluide dans un milieu poreux est celui basé sur la loi de Darcy [5]. Ce modèle lie la chute de pression à la vitesse d’infiltration dans la matrice poreuse. Cette loi phénoménologique a porté le nom de Henry Darcy qui a justifié l’hypothèse proposée par Depuit en 1854. Ce dernier fut le premier à déduire, en se basant sur des expériences faites sur des filtres à eau à Londres, que la chute de pression est proportionnelle à la vitesse d’infiltration dans la matrice poreuse.

L’application de cette loi est restreinte, seulement pour les écoulements lents et stationnaires en milieu homogène isotrope (faible nombre de Reynolds). Pour les écoulements à grande vitesse, on ne peut pas l’appliquer. Brinkman a ajouté, en 1947 [6], un terme qui tient compte des effets des contraintes visqueuses adjacentes aux parois, pour élargir le domaine de validité de cette loi et détendre son champ d’application.

2.2 Hypothèses de travail

Nous adoptons les hypothèses simplificatrices suivantes : - la matrice poreuse est isotrope et homogène,

- le fluide saturant le milieu poreux est newtonien et incompressible, - l’écoulement engendré est laminaire et bidimensionnel,

- le travail des forces visqueuses et de pression est négligeable,

- le transfert de chaleur par rayonnement est négligeable ainsi que l’interaction entre les transferts de chaleur et de masse (effets Soret et Dufour),

- les propriétés thermodynamique du fluide sont constantes et sont déterminées à partir de la température et la concentration de référence T₀et C0 respectivement. Par contre, la

28 T et la concentration C selon l’approximation de Boussinesq [7]. Cette variation est donnée

par la relation suivante :











0 0



0 1 T T T  S CC 









T

 et S sont respectivement les coefficients d’expansion thermique et massique données par: C T T ρ ρ β _          0 1 , T S C ρ ρ β _          0 1

où 0 est la densité à la température et concentration de référence.

2. 3 Expressions de la porosité et la perméabilité

Si on remplit un cylindre par des grains, on forme bien un milieu poreux, mais cette porosité change du haut du cylindre vers le bas d’une façon proportionnelle à la pression. En effet : la compressibilité isotherme de la porosité est définie par :

T

P

c

























1

Si on intègre cette équation on trouve :

_e

 0



1

_c



_P

_P

₀





v P P c









 _ 











où ε∞ est la porosité à la pression P0

Pour trouver la distribution de la pression P au sein du cylindre, on se réfère au modele de Janssen. Pour cela, on considère un récipient cylindrique qui contient de la matière granulaire et sur lequel on applique des contraintes (pression).

Une pression (ou une contrainte) verticale appliquée sur le matériau génère automatiquement une pression (contrainte) horizontale qui lui est strictement proportionnelle de sorte que:

P_h  KP_v

La relation entre La pression latérale et la pression verticale P_h : pression latéral

Pv : pression verticale

K :coefficient deproportionnalité

(2.1)

(2.2)

(2.3)

(2.4)

29 Figure1 : Récipient cylindrique servant de base au modèle de Janssen

Une tranche d'épaisseur dz, située à l'altitude h, dans un cylindre dont la section a une surface A et un périmètre P, est en équilibre sous l’action de plusieurs forces :

- le poids de la tranche de hauteur dz :

P







gAdz

e

z



- la force de pression sur cette tranche :

F

pression



A

_s

dP

_v

e

z

- les frottements avec les parois :

F frottement K



_sP_vPdzez

L'équation vectorielle correspondant à l'équilibre de la tranche considérée s'écrit :

P



F

pression



F

frottement



0



AdP

v



K



s

P

v

Pdz





gA

s

dz

P

g

A

P

K

dz

dP

v s s v

























(2.7) (2.6) (2.8) (2.9) (2.10) (2.11)

30 L’équation qui peut s’écrire sous la forme :

z A P K z A P K v s s s s

ge

e

P

dz

d

_ _ _ _



















 



Donc en intégrant cette équation, on trouve :

e

C

P

K

A

g

e

P

z A P K s s z A P K v s s s s





            





C étant une constante à déterminer en fonction des conditions initiales.

Si on suppose que le cylindre est libre à la surface c’est-à-dire (P0 = 0), la distribution de la

pression devient :

_



















       z A P K s s v s s

e

P

K

A

g

P







1

Donc si on remplace cette fonction dans l’expression (2.4), on trouve l’équation suivante :











































        z A P K s s s s

e

P

K

A

g

c

z

 



_





(

)

1

1

Figure 2 : Dépendance de la porosité en fonction de la profondeur z Porosité  z 1 1 2 3 4 5 Profondeur (2.12) (2.13) (2.14) (2.15) 

31 Il vient :                                z A P K s s s s e P K A g c z  



_





( ) 1 1

Ou encore sous la forme :

) ( ) (z





z



 

où

                         z A P K s s s s e P K A g c z   _ ( ) 1 1

La perméabilité dépend de la porosité et des diamètres des grains. Puisqu’on considère, dans une première approximation dans les études des milieux poreux, que le milieu est homogène et isotrope et que les grains sont de même taille, donc le seul facteur qui influence la perméabilité est la porosité. Dans notre travail, on a adopté le modèle de rayon hydraulique, où la perméabilité et la porosité sont liées par la relation de Carma Kozeny suivante :







ε



f

 

z K f

 

z D ε ε D ε z K g g    _     ₂ 2 3 2 2 3 1 180 1 180 ) ( On a :









2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 1 2 1 2 1 1 1                                                 χ













2 2 2 1 1 1 2 1              

















2 1 1 2 1 1               Donc :



 

 







1









2





2 2 1 1 1 1 1 _   _ C_por  C_por (2.20) (2.16) (2.17) (2.18) (2.19)

32 D’où :

 

_

 

_

_{ }

_

_

z C z C z z f por por    2 1 3 1 ) ( 1 1          (2.21) Avec :









2 1 1 2      







por C







     2 2 por C

2.4 Équations vectorielles gouvernantes d’un milieu poreux

Nous allons étudier le phénomène de la convection naturelle thermosolutale dans une cavité rectangulaire de hauteur H et de longueur L remplie d’une couche poreuse saturée par un fluide, d’une façon générale, c’est le transport de l’énergie et de la chaleur d’un milieu chaud vers un milieu moins chaud. Ce transport est dû à une variance de la densité du fluide en contact avec les deux sources. La résolution d’un tel problème consiste en la détermination des champs des vitesses, de température et de concentration en chaque point de la cavité occupée par le fluide considéré. Dans ce qui suit, nous allons établir les équations qui gouvernent ce phénomène de convection naturelle dans une matrice poreuse afin d’étudier le processus de transfert de l’énergie par ces mouvements convectifs du fluide.

2.4.1 Equation de continuité

L’équation de continuité s’écrit : div

 

V 0

L’égalité qui peut encore s’écrire : 0       z w x u avec : V uex wez     

où u et w sont les composants de la vitesse horizontale et axiale (2.29)

(2.30)

(2. 31)

33

2.4.2 Équation de conservation de la quantité de mouvement en milieu poreux

On utilise un modèle continu d'un milieu poreux basé sur le concept du volume élémentaire représentatif pour bien décrire le bilan de quantité de mouvement d'un fluide visqueux Newtonien en milieu poreux.

L'équation vectorielle de conservation de la quantité de mouvement à travers un milieu poreux s'écrit : V p g C C T T V K V V t V C T                                           0 0 0 0 0 1 )) ( ) ( 1 ( . 1 

V _{: Champ des vitesses de Darcy}

a : représentes les forces inertielles macroscopiques, b : terme de Darcy,

c : les forces de volume, d : le gradient de pression,

e : le terme visqueux de Brinkman.

Dans les écoulements bidimensionnels de convection naturelle, il est plus commode d’utiliser la formulation vorticité-fonction de courant pour éliminer la pression pour laquelle nous ne possédons aucune information.

Cette formulation consiste à remplacer les variables primitives pression et vitesse par la composante non nulle du vecteur rotationnel de la vitesse et la fonction de courant .

Pour éliminer la pression et faire apparaître le vecteur on applique l’opérateur rotationnel à l’équation (2.32) : ) ( ) 1 ( ) )) ( ) ( 1 ( ( ) ( ) . ( ) 1 ( 0 0 0 0 0 V K rot p rot g C C T T rot V K rot V V rot t V rot     T   C                          

En développant chacun des termes de l’équation (2.33), on obtient :

) 1 ( 1 ) 1 ( ) ( 1 ) 1 (                              t V t t V t V rot t V rot a b c d e (2. 32) (2. 33) (2. 34)