Approche matricielle de l'opérateur de propagation des ondes ultrasonores en milieu diffusant aléatoire
Texte intégral
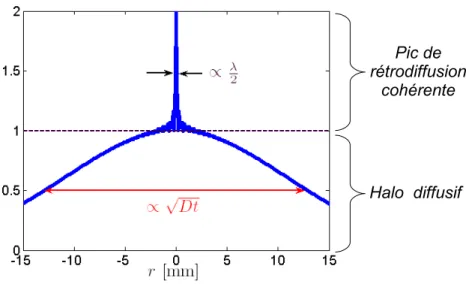
Figure
![Fig. I.8: Conditions aux limites `a appliquer sur l’intensit´e dans le cas d’une tranche semi-infinie l’intensit´e s’´ecrivent [25] : P + z 0 ∂P ∂z = 0, en z = L P − z 0 ∂P ∂z = 0, en z = 0](https://thumb-eu.123doks.com/thumbv2/123doknet/2294890.23901/35.892.126.701.119.457/conditions-limites-appliquer-intensit-tranche-infinie-intensit-ecrivent.webp)
Outline
Documents relatifs
– Définir quelques grandeurs physiques associées à une onde sonore ou ultrasonore : pression acous- tique, amplitude, célérité, période, fréquence, lon- gueur d’onde1.
Le but du travail présenté dans ce mémoire est d’étudier à petite échelle en milieu confiné, le comportement des ondes de choc ainsi que les quatre
Remarque sur la propagation des ondes thermiques sinusoïdales dans un milieu hétérogène..
La principale source d’erreur réside dans la mesure de la position du récepteur (lecture sur la règle, positionnement du récepteur dans la règle, repérage du signal identique
Pour ce qui concerne les mesures d'attenuation ultrasonore, le comportement general en fonction de la frequence est le m6me pour les aerogels I et I1 : dans la region spectrale
d’onde h étant liée à la célérité C dans le milieu par la relation bien connue 03BB = C/F (F étant la fréquence ultrasonore), nous avons cherché à employer
,Dans ce cas du champ magnétique purement longitudinal il y a indépendance des modes longi-. tudinaux et
Ainsi la frange du 3e ordre, absente pour l’inci- dence rasante, apparaît pour une incidence égale à l’angle de réflection de Bragg correspondant au. 1er ordre,